 |
MPHELL
4.0.0
|
 |
MPHELL
4.0.0
|
Let 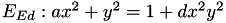 be a twisted Edwards elliptic curve under affine coordinates. Under Projective coordinates
be a twisted Edwards elliptic curve under affine coordinates. Under Projective coordinates  becomes
becomes  . The triplet
. The triplet  represents the affine point
represents the affine point 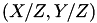 .
.
Under Jacobian coordinates 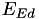 becomes
becomes 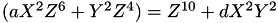 . The triplet
. The triplet 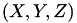 represents the affine point
represents the affine point 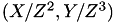 .
.
Under Extended twisted Edwards coordinates 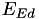 becomes
becomes 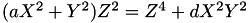 . The quadruplet
. The quadruplet 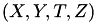 represents the affine point
represents the affine point 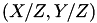 , the auxiliary coordinate T has the property
, the auxiliary coordinate T has the property 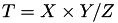 .
.
Edwards elliptic curves are twisted Edwards elliptic curves with 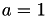 so we work here with Twisted Edwards elliptic curves.
so we work here with Twisted Edwards elliptic curves.
Let
The point P3 = (X3,Y3,Z3) = P1 + P2 is given by
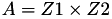
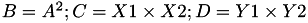
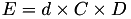
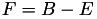
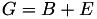
![$ X3 = A \times F \times [(X1 + Y1) \times (X2 + Y2) - C - D] $](form_154.png)
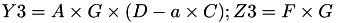
using 10 multiplications, 1 square, 1 times a, 1 times d, 7 additions .
This formula is taken from [BBL+08, §6] Twisted edwards curves by Daniel. J. Bernstein, Peter Birkner, Marc Joye, Tanja Lange, and Christiane Peters (2008, June) published in International Conference on Cryptology in Africa (pp. 389-405). Springer, Berlin, Heidelberg viewable at this adress https://link.springer.com/
This formula can be viewed on this website http://www.hyperelliptic.org where it is called "add-2008-bbjlp".
It is important to notice that this formula for addition is strongly unified.
The point P3 = (X3,Y3,Z3) = 2 P1 is given by
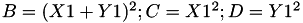
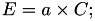
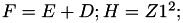
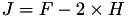
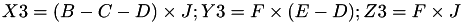
using 3 multiplications, 4 squares, 1 times a, 6 additions, 1 times 2 .
This formula is taken from [BBL+08, §6] Twisted edwards curves by Daniel. J. Bernstein, Peter Birkner, Marc Joye, Tanja Lange, and Christiane Peters (2008, June) published in International Conference on Cryptology in Africa (pp. 389-405). Springer, Berlin, Heidelberg viewable at this adress https://link.springer.com/
This formula can be viewed on this website http://www.hyperelliptic.org where it is called "dbl-2008-bbjlp".
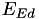 becomes
becomes 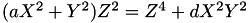 .
.
Let
This formula is taken from [HWCD08, §3.2] Twisted Edwards Curves Revisited by Hisil, Wong, Carter and Dawson published in Asiacrypt volume 5350, pages 326-343 viewable at this adress https://link.springer.com/ .
The point P3 = (X3,Y3,T3,Z3) = P1 + P2 is given by
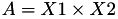

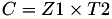
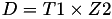
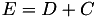
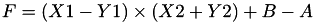

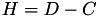
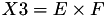
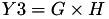
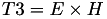
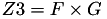
using 9 multiplications, 1 times a and 7 additions.
One can notice that those formulas are independant of the curve constant d.
This formula can be viewed on the website http://www.hyperelliptic.org and is called "add-2008-hwcd-2"
This formula is taken from [HWCD08, §3.3] Twisted Edwards Curves Revisited by Hisil, Wong, Carter and Dawson published in Asiacrypt volume 5350, pages 326-343 viewable at this adress https://link.springer.com/ .
The point P3 = (X3,Y3,T3,Z3) = P1 + P1 is given by
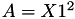

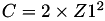
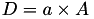
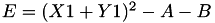
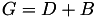
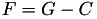

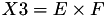
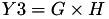
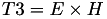
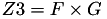
using 4 multiplications + 4 squares + 1 times a constant 6 additions and 1 doubling.
This formula can be viewed on the website http://www.hyperelliptic.org and is called "dbl-2008-hwcd"
This formula is taken from [HWCD08, §3.1] Twisted Edwards Curves Revisited by Hisil, Wong, Carter and Dawson published in Asiacrypt volume 5350, pages 326-343 viewable at this adress https://link.springer.com/ .
The point P3 = (X3,Y3,T3,Z3) = P1 + P2 is given by
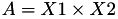

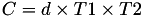
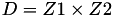
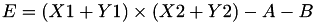
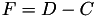
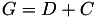
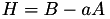
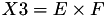
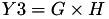
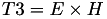
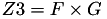
using 9 multiplications,1 times a, 1 times d and 7 additions.
This formula can be viewed on the website http://www.hyperelliptic.org and is called "add-2008-hwcd"
 1.8.15
1.8.15