 |
MPHELL
4.0.0
|
 |
MPHELL
4.0.0
|
These formulas are derived from the paper [BJ03] "The Jacobi Model of an Elliptic Curve and Side-Channel Analysis" written by Olivier Billet and Marc Joye published in International Symposium on Applied Algebra, Algebraic Algorithms, and Error-Correcting Codes. Springer, Berlin, Heidelberg, 2003. p. 34-42 viewable at this address https://link.springer.com/ .
Let 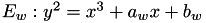 a Weierstrass elliptic curve.
a Weierstrass elliptic curve.
Let 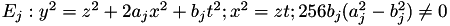 an extended Jacobi Quartic elliptic curve.
an extended Jacobi Quartic elliptic curve.
For 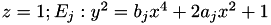 which can be extented to the Jacobi Quartic (with Projective equation)
which can be extented to the Jacobi Quartic (with Projective equation) 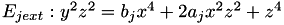
The coefficients 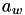 and
and 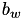 of the Weiertrass elliptic curve
of the Weiertrass elliptic curve 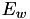 matching the Jacobi Quartic elliptic curve
matching the Jacobi Quartic elliptic curve 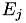 are:
are:
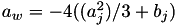
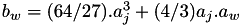
A point 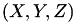 of
of  can be converted to a point
can be converted to a point 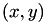 of
of 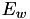 with
with
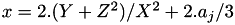
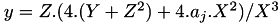
Let 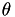 such that
such that 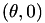 is a 2-torsion point the Weierstrass elliptic curve
is a 2-torsion point the Weierstrass elliptic curve 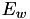 .
.
The coefficients 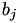 and
and 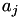 of the (extended) Jacobi Quartic
of the (extended) Jacobi Quartic  matching the Weiertrass elliptic curve
matching the Weiertrass elliptic curve 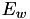 are:
are:
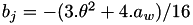

A point 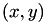 of
of 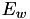 can be converted to a point
can be converted to a point 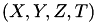 of
of 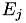 with
with
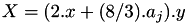
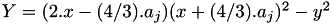
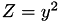
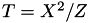
Those formulas are corrected formulas of [BJ03,§3]. More details are available in [BJ03,§3].
 1.8.15
1.8.15