 |
MPHELL
4.0.0
|
 |
MPHELL
4.0.0
|
The main idea between those conversion is to go through Montgomery curves, id est make a conversion from Short Weierstrass to Montgomery curves and then to Twisted Edwards Curves.
The Montgomery curves are in bijection with Twisted Edwards Curves, making this step the easiest one.
The Weierstrass curves have an isomorphism over a field K to a Montgomery curve when the Weierstrass curve has the 2 torsion defined over the field K, this isomorphism is determined under some conditions by the choice of a 2 torsion point and a sign choice.
The three main references for this part are:
First of all to make this conversion from Short Weierstrass to Mongomery model it is needed to compute a point of order 2: 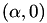 such that there exists beta in the field K which verifies:
such that there exists beta in the field K which verifies:
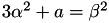
Thus it is possible when there are 3 points of order 2 defined in K that only one of them satisfies this condition, some examples can be found in the vector tests of this software.
We denote the representations:
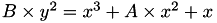 for the Montgomery curve
for the Montgomery curve 
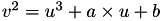 for the Short Weierstrass curve
for the Short Weierstrass curve 
Then the choice of 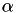 and
and 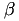 determines the following isomorphism between a Short Weierstrass curve and a Montgomery curve:
determines the following isomorphism between a Short Weierstrass curve and a Montgomery curve:
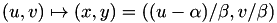 for the Montgomery curve
for the Montgomery curve 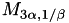
For the reverse isomorphism id est the one from the Montgomery Curve 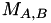 to the (unique) corresponding Short Weierstrass curve we have:
to the (unique) corresponding Short Weierstrass curve we have:
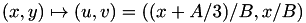 for the Sort Weierstrass curve
for the Sort Weierstrass curve 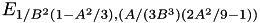
It can be easier for the reader to understand this isomorphism to have in mind that
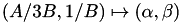
and using the fact we have then to solve the followings two equations to find a and b:

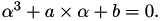
More details are in [CS17,§2.4], [OKS00,§4].
We denote the representations:
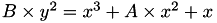 for the Montgomery curve
for the Montgomery curve 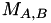
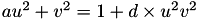 for the Twisted Edwards curve
for the Twisted Edwards curve 
For the isomorphism from a Montgomery curve 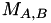 to a twisted Edwards curve we use the following isomorphism:
to a twisted Edwards curve we use the following isomorphism:
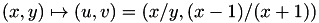 for the twisted Edwards curve
for the twisted Edwards curve 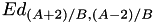
The reverse isomorphism from the twisted Edwards curve 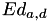 to a Montgomery curve is:
to a Montgomery curve is:
 for the Montgomery curve
for the Montgomery curve 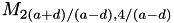 .
. More details are in [CS17,§2.5], [BBL+08,§3].
 1.8.15
1.8.15