Chapitre 9  Exercices de combinatoire

9.1  Fonction partage ou nombre de partitions de n∈ ℕ

9.1.1  L’énoncé

Définition
Un partition de n∈ ℕ est une suite de nombres entiers : λ₁≥ λ₂≥ ...λ_m>0 tels que : ∑_j=1^mλ_j =n.
On note p(n) la fonction partage de n : c’est le nombre de partitions distinctes de n∈ ℕ et on convient que p(0)=1.
Exemples
p(5)=7 car les 7 partitions distinctes de 5 sont :
1+1+1+1+1=5
2+1+1+1=5
2+2+1=5
3+1+1=5
3+2=5
4+1=5
5=5

1. Chercher à la main : p(1),p(2),p(3),p(4),p(5),p(6),p(7)
2. Écrire un programme qui renvoie les valeurs de p(0),p(1),p(2),p(3)..p(n)
3. Montrer ce que Euler a remarqué à savoir que le développement en séries tronqué à l’ordre n de : ∏_j=1ⁿ1/1−x^j vaut ∑_j=1ⁿp(j)x^j.
4. Écrire un programme qui renvoie les coefficients du développement en séries tronqué à l’ordre n de : ∏_j=1ⁿ1/1−x^j

9.1.2  La solution

1. On trouve :
   p(0)=1, p(1)=1, p(2)=2, p(3)=3, p(4)=5, p(5)=7, p(6)=11, p(7)=15
2. Soit A une matrice triangulaire inférieure tel que :
   si k≤ j, A[j,k] represente le nombre de partitions de j tel que λ₁=k≥ λ₂≥ ...λ_m>0. Sur l’exemple
   p(5)=7 car les 7 partitions distinctes de 5 sont :
   1+1+1+1+1=5 donc A[5,1]=1
   2+1+1+1=5
   2+2+1=5 donc A[5,2]=2
   3+1+1=5
   3+2=5 donc A[5,3]=2
   4+1=5 donc A[5,4]=1
   5=5 donc A[5,5]=1
   On a alors p(j)=∑_k=0^jA[j,k].
   On remarque donc :
   A[0,0]=1 et A[j,0]=0 (car λ_m>0 sauf pour j=0 puisque p(0)=1)
   A[j,j]=1 puisque j=j
   A[j,1]=A[j−1,1]=1 puisque j=j−1+1=j−2+1+1=1+1...+1
   A[j,2]=A[j−2,1]+A[j−2,2] puisque j=2+1+1+...=2+2+....
   A[j,3]=A[j−3,1]+A[j−3,2]+A[j−3,3] puisque j=3+1+1+...1=3+2+....=3+3+....
   etc...
   A[j,j−1]=A[j−1,j−1]=1 puisque j=(j−1)+1
   ou encore :
   les coefficients d’indice 0 de toutes les lignes sont nuls et
   pour k=1..n le coefficient d’indice k de la n-ième ligne est obtenu en faisant la somme des coefficients d’indice 0..k de la n−k-ième ligne c’est à dire :

   A[n,k]=

   k ∑ j=1

   A[n−k,j]  et

   A[n,n]=1   et  A[n,0]=0  si  n>0

   Voici l’illustration pour n=5 avec
   k=2, on a 5=0+1+4 :
   k=3, on a 8=0+1+3+4 :
   k=4, on a 9=0+1+3+3+2 :
   ....

   ⎛ ⎜ ⎜ ⎜ ⎜ ⎜ ⎜ ⎜ ⎜ ⎜ ⎜ ⎜ ⎜ ⎜ ⎜ ⎜ ⎜ ⎜ ⎜ ⎜ ⎜ ⎜ ⎜ ⎜ ⎜ ⎜ ⎜ ⎜ ⎜ ⎜ ⎜ ⎜ ⎜ ⎜ ⎝

   1 0 0 0 0 0 0 0 0 0 0 |    0 1 0 0 0 0 0 0 0 0 | 0    0 1 1 0 0 0 0 0 0 | 0 0    0 1 1 1 0 0 0 0 | 0 0 0    0 1 2 1 1 0 0 | 0 0 0 0    0 1 2 2 1 1 | 0 0 0 0 0    0 1 3 3 2 | 1 1 0 0 0 0    0 1 3 4 | 3 2 1 1 0 0 0    0 1 4 | 5 5 3 2 1 1 0 0  0 1 | 4 7 6 5 3 2 1 1 0  0 1 5 8 9 7 5 3 2 1 1

   ⎞ ⎟ ⎟ ⎟ ⎟ ⎟ ⎟ ⎟ ⎟ ⎟ ⎟ ⎟ ⎟ ⎟ ⎟ ⎟ ⎟ ⎟ ⎟ ⎟ ⎟ ⎟ ⎟ ⎟ ⎟ ⎟ ⎟ ⎟ ⎟ ⎟ ⎟ ⎟ ⎟ ⎟ ⎠

   On va faire un programme qui va calculer les coefficients de la matrice A.

   On tape :

   partitions(n):={
     local A,j,k,m,S;
     A:=idn(n+1);
     pour j de 2 jusque n faire
       pour k de 1 jusque j-1 faire
         S:=0;
         pour m de 1 jusque k faire
           S:=S+A[j-k,m];
         fpour;
         A[j,k]:=S;
       fpour;
     fpour;
     retourne A;
   }:;
   

   On tape : A:=partitions(10)
   On obtient :

   ⎛ ⎜ ⎜ ⎜ ⎜ ⎜ ⎜ ⎜ ⎜ ⎜ ⎜ ⎜ ⎜ ⎜ ⎝

   1 0 0 0 0 0 0 0 0 0 0  0 1 0 0 0 0 0 0 0 0 0  0 1 1 0 0 0 0 0 0 0 0  0 1 1 1 0 0 0 0 0 0 0  0 1 2 1 1 0 0 0 0 0 0  0 1 2 2 1 1 0 0 0 0 0  0 1 3 3 2 1 1 0 0 0 0  0 1 3 4 3 2 1 1 0 0 0  0 1 4 5 5 3 2 1 1 0 0  0 1 4 7 6 5 3 2 1 1 0  0 1 5 8 9 7 5 3 2 1 1

   ⎞ ⎟ ⎟ ⎟ ⎟ ⎟ ⎟ ⎟ ⎟ ⎟ ⎟ ⎟ ⎟ ⎟ ⎠

   On tape : sum(A[k])$(k=0..10)
   On obtient : 1,1,2,3,5,7,11,15,22,30,42

   On peut faire un autre programme qui renverra la matrice B qui sera tel que : si k≤ j, A[j,k] represente le nombre de partitions de j tel que k>=λ₁≥ λ₂≥ ...λ_m>0. Autrement dit les lignes de B sont les sommes partielles des lignes de A : B[j,k]=∑_m=0^kA[j,m] donc

   B[j,k]=B[j−k,k]+B[j,k−1]

   On a donc p(j)=B[j,j].
   On tape :

   partition(n):={
     local B,j,k,m,S;
     B:=idn(n+1);
     pour k de 1 jusque n faire
       B[0,k]:=1;
     fpour;
     pour j de 1 jusque n faire
       pour k de 1 jusque j faire
         B[j,k]:=B[j-k,k]+B[j,k-1];
       fpour;
       pour k de j+1 jusque n faire
         B[j,k]:=B[j,j];
       fpour;
     fpour;
     retourne B;
   }
   :;
   

   On tape : B:=partition(10)
   On obtient :

   ⎛ ⎜ ⎜ ⎜ ⎜ ⎜ ⎜ ⎜ ⎜ ⎜ ⎜ ⎜ ⎜ ⎜ ⎝

   1 1 1 1 1 1 1 1 1 1 1  0 1 1 1 1 1 1 1 1 1 1  0 1 2 2 2 2 2 2 2 2 2  0 1 2 3 3 3 3 3 3 3 3  0 1 3 4 5 5 5 5 5 5 5  0 1 3 5 6 7 7 7 7 7 7  0 1 4 7 9 10 11 11 11 11 11  0 1 4 8 11 13 14 15 15 15 15  0 1 5 10 15 18 20 21 22 22 22  0 1 5 12 18 23 26 28 29 30 30  0 1 6 14 23 30 35 38 40 41 42

   ⎞ ⎟ ⎟ ⎟ ⎟ ⎟ ⎟ ⎟ ⎟ ⎟ ⎟ ⎟ ⎟ ⎟ ⎠

   On remarquera que l’on retrouve la matrice A dans les diagonales montantes de la matrice B.
   On tape : tran(B)[10]
   ou on tape : col(B,10)
   On obtient : [1,1,2,3,5,7,11,15,22,30,42] ou on tape : B[j,10]$(j=0..10)
   On obtient : 1,1,2,3,5,7,11,15,22,30,42 On tape : B:=partition(1000):;
   On obtient (Evaluation time: 972.05) enfin le résultat...
   On tape : B[200,1000]
   On obtient 3972999029388
   On tape : B[1000,1000]
   On obtient 24061467864032622473692149727991
   Remarque On peut aussi pour avoir une relation de récurrence considérer les les partitions P(n,p) de n en une somme d’exactement p éléments λ₁≥ ...≥ λ_p>0. On dit alors :
   P(n,p) =(nombre de partage de n tels que λ_p=1)+(nombre de partage de n tels que λ_p>1).
   On a :
   (nombre de partage de n tels que λ_p=1)=(nombre de partage de n−1 en p−1 λ_j)=P(n−1,p−1)
   (nombre de partage de n tels que λ_p>1)=(nombre de partage de n−p en p λ_j)=P(n−p,p)
   

   P(n,p):=P(n−1,p−1)+P(n−p,p)

   avec P(n,0)=0, P(n,n)=1 et P(n,p)=0 si p>n
   On tape et on renvoie la somme des lignes de P :

   partage(n):={
     local P,j,k,m,S;
     P:=idn(n+1);
     pour k de 1 jusque n faire
       P[k,0]:=0;
     fpour;
     pour j de 1 jusque n faire
       pour k de 1 jusque j faire
         P[j,k]:=P[j-1,k-1]+P[j-k,k];
       fpour;
     fpour;
     S:=[];
     pour k de 1 jusque n faire
       S[k]:=sum(row(P,k));
     fpour;
     retourne S;
   }:;
   

   On tape : P:=partage(1000):;
   On obtient (Evaluation time: 455.81) enfin le résultat...mais c’est deux fois plus rapide qu’avec B:=partition(1000):;
   On tape : P[200]
   On obtient 3972999029388
   On tape : P[1000]
   On obtient 24061467864032622473692149727991
   relation entre P et A :
   On a :
   P[n,p]=P[n−1,p−1]+P[n−p,p]
   P[n−1,p−1]=P[n−2,p−2]+P[n−p,p−1]....
   donc

   P[n,p]= P[n−p,0]+

   p ∑ j=1

   P[n−p,j]

   avec P[n,0]=0, P[n,n]=1 et P[n,p]=0 si p>n
   Si on compare avec les relations obtenus pour A:
   

   A[n,k]=

   k ∑ j=1

   A[n−k,j]  et

   A[n,n]=1   et  A[n,0]=0  si  n>0

   On a les mêmes relations de récurrence, donc :

   P[n,p]=A[n,p]

   Représentation de Young
   On peut voir facilement cette égalité, grâce à la repésentation de Young qui repésente par exemple le partage :
   20=7+3+3+2+1+1+1+1+1
   par le tableau formé par 20 carrés disposés selon 9 lignes :
   7 carrés sur la 1-ière ligne,
   3 carrés sur la 2-ième ligne,
   3 carrés sur la 3-ième ligne,
   2 carrés sur la 4-ième ligne,
   1 carré sur de la 5-ième jusqu’à la 9-ième ligne :

   ⎡ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎣

   □ □ □ □ □ □ □  □ □ □         □ □ □         □ □           □             □             □             □             □

   ⎤ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎦

   Le nombre p de lignes correspond a un partage en une somme de p éléments et le plus grand élément m de ce partage est le nombre d’éléments de la première ligne.
   Si maintenant on échange les lignes et les colonnes (on prend le transposé de ce tableau) on obtient une transformation qui au partage :
   20=7+3+3+2+1+1+1+1+1 en une somme de 9 termes ayant comme plus grand élément 7 fait correspondre le partage :
   20=9+4+3+1+1+1+1 en une somme de 7 termes ayant comme plus grand élément 9 :

   ⎡ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎣

   □ □ □ □ □ □ □ □ □ □ □ □ □           □ □ □             □                 □                 □                 □

   ⎤ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎦

3. Notations
   1 sera noté 1₁, 1+1 sera noté 2₁, 1+1+1 sera noté 3₁ etc...
   2 sera noté 2₂, 2+2 sera noté 4₂, 2+2+2 sera noté 6₂ etc...
   Le développement en série de ;
   1/1−x¹ sera noté 1+x^1₁+x^2₁+...+x^n₁+...
   1/1−x² sera noté 1+x^2₂+x^4₂+...+x^2n₂+...
   1/1−x³ sera noté 1+x^3₃+x^6₃+...+x^3n₃+...
   .....
   1/1−x^p sera noté 1+x^p_p+x^2p_p+...+x^pn_p+...
   Lorsque l’on fait le produit de ces développements en série le terme en x^j a pour coefficient p(j) car :
   x^j=x^j₁=x^(j−2)₁x^2₂=x^(j−4)₁x^4₂ ...
   x^j=x^{(j−2)_j−2}x^2₁=x^{(j−2)_j−2}x^2₂=x^{(j−1)_j−1}x^1₁=x^j_j

   On tape : P:=truncate(product([(1-x^j)$(j=1..20)]),20)
   On obtient : -x^15-x^12+x^7+x^5-x^2-x+1
   On tape : A:=truncate(series(1/P,x=0,20),20)
   On obtient :
   627*x^20+490*x^19+385*x^18+297*x^17+231*x^16+176*x^15+ 135*x^14+101*x^13+77*x^12+56*x^11+42*x^10+30*x^9+22*x^8+ 15*x^7+11*x^6+7*x^5+5*x^4+3*x^3+2*x^2+x+1
   On tape :symb2poly(A)
   ou on tape : coeff(A,x)
   On obtient la liste p(20),p(19),..,p(1),p(0):
   [627,490,385,297,231,176,135,101,77,56,42,30,22,15,11, 7,5,3,2,1,1]
   On tape :lcoeff(A)
   On obtient p(20): 627
   

4. On tape mais cela n’est pas très efficace lorsque n est grand :

   partitioner(n):={
   local A,P;
   P:=truncate(product([(1-x^j)$(j=1..n)]),n);
   A:=truncate(series(1/P,x=0,n),n);
   return revlist(symb2poly(A));
   }:;
   

   On tape : partitioner(20)
   On obtient la liste p(20),p(19),..,p(1),p(0) :
   [627,490,385,297,231,176,135,101,77,56,42,30,22,15,11, 7,5,3,2,1,1]

9.1.3  Une méthode plus rapide

On utilise le théorème du nombre pentagonal d’Euler. Ce théorème donne une relation de récurrence entre p(n) et p(j) pour j<n avec la convention que p(j)=0 lorsque j<0, p(0)=1. Cette relation est :

Les nombres m(3m−1)/2 et m(3m+1)/2 sont les nombres pentagonaux généralisés. On tape :

partition_euler(n):={
local sg,s1,s2,m,k,j,p;
p:=[1];
pour j de 1 jusque n faire
m:=1;
sg:=1;
s1:=0;
k:=j-m*(3*m-1)/2;
tantque k>=0 faire 
s1:=s1+sg*p[k]
sg:=-sg;
m:=m+1;
k:=j-m*(3*m-1)/2;
ftantque;
m:=1;
sg:=1;
s2:=0;
k:=j-m*(3*m+1)/2;
tantque k>=0 faire 
s2:=s2+sg*p[k]
sg:=-sg;
m:=m+1;
k:=j-m*(3*m+1)/2;
ftantque;
p[j]:=s1+s2;
fpour;
retourne p;
}:;

On tape :
partition_euler(20)
On obtient :
[1,1,2,3,5,7,11,15,22,30,42,56,77,101,135,176,231,297,385,490,627]
On tape :
P:=partition_euler(1000)
On obtient la liste après 2.77s
On tape : P[200]
On obtient 3972999029388
On tape : P[1000]
On obtient 24061467864032622473692149727991

9.1.4  Estimation asymptotique

Ramanjan et Hardy ont trouvé une approximation de p(n) qui est :
p(n)≃ e^π√2n/3/4n√3 quand n tend vers +∞.
On tape :
P(n):=exp(pi*sqrt(2n/3))/(4n*sqrt(3))
floor(evalf(P(1000),31))
On obtient :
24401996316802476288263414942904 au lieu de
24061467864032622473692149727991

9.2  Un exercice de combinatoire et son programme

9.2.1  L’énoncé

Un jury est composé de p personnes que l’on choisit parmi n personnes : h hommes et f femmes (h+f=n).
Application numérique : p=10, n=17, h=9, f=8.

1. Écrire un programme qui renvoie la liste contenant les différents jurys possibles.
2. On impose comme contrainte que Monsieur Y et Madame X ne doivent pas se trouver ensemble.
   Écrire un programme qui renvoie la liste contenant tous les jurys respectant cette contrainte.
3. On veut que le jury respecte la parité "homme-femme".
   Pour cela, si p=2*k ou p=2*k+1, on suppose f≥ k et h=n−f ≥ p−k.
   Écrire un programme qui renvoie la liste contenant les jurys ayant p−k hommes et k femmes.
4. Avec l’hypothèse précédente, écrire un programme qui renvoie la liste contenant les jurys respectant la parité "homme-femme" et respectant la contrainte Monsieur Y et Madame X ne doivent pas se trouver ensemble.
   
5. Rappels Avec Xcas, la commande comb(n,p) renvoie le nombre de combinaisons de p objets pris parmi n.
   Avec Xcas, la commande convert(k,base,2) renvoie la liste K de longueur l vérifiant k=∑_j=0^l−1K[j]*2^j. revlist(K) renvoie alors l’écriture en base 2 de k.

9.2.2  Les programmes

1. On peut avoir comb(n,p) jurys différents.
   On tape : comb(17,10)
   On obtient : 19448
   Supposons que n cases C numérotées de 0 à n−1 représentent les membres du jury.
   Dans ces cases on met 1 si la personne fait partie du jury et 0 sinon. Un jury est donc une liste de 0 et de 1 et cela fait penser à l’écriture en base 2 d’un entier.
   Avec Xcas, la commande convert(k,base,2) renvoie la liste K de longueur l vérifiant k=∑_j=0^l−1K[j]*2^j On va donc considérer un jury comme un entier dont l’écriture en base 2 a au plus n chiffres et comporte exactement p 1. Pour faire le programme on va repésenter chaque jury par un nombre dont l’écriture en base 2 comporte au plus n chiffres dont p 1 et pas plus de n−p zéros.
   Le plus petit nombre correspondant à un jury est :
   m=sum(2^j,j,0,p-1)=2^p-1
   et le plus grand nombre correspondant à un jury est :
   M=sum(2^j,j,n-p,n-1)=2^n-2^(n-p)
   car les n cases sont numerotés de 0 à n−1.
   On peut initialiser la liste L soit avec L:=makelist(0,1,1); soit avec L:=makelist(0,1,comb(n,p)); puisque l’on connait sa longueur. On écrit le programme jurys(n,p) :

   jurys(n,p):={
   local j,k,L,m,M;
   //L:=makelist(0,1,comb(n,p));
   L:=makelist(0,1,1);
   k:=0;
   m:=2^p-1;
   M:=2^n-2^(n-p);
   for (j:=m;j<=M;j++){
   if (sum(convert(j,base,2))==p){
   L[k]=<j;
   k:=k+1;
   };
   }
   return L;
   }
   :;
   

   On tape : J:=jurys(17,10):;
   On obtient, au bout d’environ 11s, une liste J de taille 19448 et contenant des entiers qui lorsqu’on les décompose en base 2 donne la composition du jury.
   On tape : jurytire0:=J[rand(19448)]
   On obtient par exemple : 127255
   On tape : convert(127255,base,2)
   On obtient par exemple : [1,1,1,0,1,0,0,0,1,0,0,0,1,1,1,1,1]
   Donc, les personnes de numéros : 0,1,2,4,8,12,13,14,15,16 ont été tirées au sort pour faire partie du jury.
   On peut bien sûr taper directement :
   jurytire0:=convert(J[rand(19448)],base,2)
   On obtient par exemple : [1,0,0,0,1,1,1,0,1,1,1,0,0,1,0,1,1]
   Donc, les personnes de numéros : 0,4,5,6,8,9,10,13,15,16 ont été tirées au sort pour faire partie du jury.
   
2. On peut supposer que la case 0 représente Monsieur Y et que la case n−1 représente Madame X. Donc le jury repésenté par le nombre j est valable si :
   irem(j,2)==0 ou si j<2^(n-1).
   On peut réecrire un programme jurysXY(n,p) qui utilise jurys ou un programme juryXY(n,p) qui n’utilise pas jurys ou utiliser la liste précédente J et rejeter les mauvais tirages.
   • Le programme jurysXY(n,p).
     On peut initialiser la liste L, soit avec
     L:=makelist(0,1,1); soit avec
     L:=makelist(0,1,comb(n,p)-comb(n-2,p-2)); puisque l’on connait sa longueur.

     jurysXY(n,p):={
     local LP,L,j,k,l;
     LP:=jurys(n,p);
     s:=comb(n,p);
     l:=s-comb(n-2,p-2);
     //L:=makelist(0,1,1);
     L:=makelist(0,1,l);
     l:=0;
     for(k:=0;k<s;k++){
     j:=LP[k];
     if (irem(j,2)==0 or j<2^(n-1)) {
     L[l]=<j;
     l:=l+1;
     }
     }
     return L;
     }:;
     

     On tape : JXY:=jurysXY(17,10)
     On a : size(JXY)=13013
     On tape : jurytire1:=convert(JXY[rand(13013)],base,2)
     On obtient par exemple : [0,1,1,0,1,1,1,1,1,0,0,0,1,0,1,0,1]
     Mais ce programme appelle le programme jurys précédent....
   • Un programme juryXY(n,p) qui n’utilise pas jurys
     Les nombres qui correspondent aux jurys ne contenant pas X et Y en même temps ont dans la décomposition en base 2 soit le coefficient de 2ⁿ⁻¹ nul, soit est un nombre pair avec le coefficient de 2ⁿ⁻¹ égal à 1 donc égal à 2*j+2ⁿ⁻¹.
     Les nombres qui ont p 1 dans leur décomposition en base 2 et le coefficient de 2ⁿ⁻¹ nul, vont de m=2^p−1 à M=2⁽n−1)−2⁽n−p−1).
     Les nombres pairs de la forme 2*j+2ⁿ⁻¹ ont j qui a p−1 1 dans sa décomposition en base 2. Les j vont donc de 2^p−2 à 2⁽n−1)−2⁽n−p) par pas de 2.
     On peut initialiser la liste L soit avec L:=makelist(0,1,1); soit avec L:=makelist(0,1,comb(n,p)-comb(n-2,p-2)); puisque l’on connait sa longueur.On tape le programme juryXY(n,p)

     juryXY(n,p):={
     local L,j,k,ls,m,M;
     s:=comb(n,p);
     l:=s-comb(n-2,p-2);
     L:=makelist(0,1,l);
     //L:=makelist(0,1,1);
     k:=0;
     m:=2^p-1;
     M:=2^(n-1)-2^(n-p-1);
     for(j:=m;j<=M;j++){
     if (sum(convert(j,base,2))==p){
     L[k]=<j;
     k:=k+1;
     }
     }
     M:=2^(n-1)-2^(n-p);
     for(j:=m-1;j<=M;j:=j+2){
     if (sum(convert(j,base,2))==p-1){
     L[k]=<j+2^(n-1);
     k:=k+1;
     }
     }
     return L;
     }:;
     

     On tape : JXY:=juryXY(17,10)
     On a : size(JXY)=13013
     On tape : jurytire2:=convert(JXY[rand(13013)],base,2)
     On obtient par exemple : [1,1,1,0,0,1,1,0,0,0,1,1,1,1,0,1]
     
   • programme jurytireXY(J) qui se sert de la liste J obtenue précédemment (J:=jurys(17,10):;)
     On tape :

     jurytireXY(J):={
     local k,n,(s:=size(J));
     n:=size(convert(J[s-1],base,2));
     k:=1+2^(n-1);
     while (irem(k,2)!=0 and k>=2^(n-1)){
     k:=J[rand(s)];
     }
     return k;
     }
     

     On tape : jurytireXY(J) On obtient par exemple : 54762
     On tape : convert(109242,base,2)
     On obtient : [0,1,0,1,1,1,0,1,0,1,0,1,0,1,0,1,1]
3. On peut supposer que les cases de 0 à h−1 représentent les hommes et que les cases de h à n−1 représentent les femmes. On écrit un nouveau programme jury55(h,f,p) qui utilise le programme jurys(n,p) écrit précédemment ou on se sert de la liste J trouvée précedemment.
   • Le programme jury55(h,f,p).
     On peut initialiser la liste L soit avec
     L:=makelist(0,1,1); soit avec
     L:=makelist(0,1,comb(h,5)*comb(f,5));
     puisque l’on connait sa longueur.

     jury55(h,f,p):={
     local L,j,k,M,F,l,p2;
     p2:=iquo(p,2);
     L:=makelist(0,1,1);
     //L:=makelist(0,1,comb(h,5)*comb(f,5));
     M:=jurys(h,p-p2);
     F:=jurys(f,p2)*2^h;
     l:=0;
     for(j:=0;j<comb(h,p-p2);j++){
     for(k:=0;k<comb(f,p2);k++){
     L[l]=<M[j]+F[k];
     l:=l+1;
     }
     }
     return L
     }:;
     

     J55:=jury55(9,8,10)
     size(J55)=7056
     On tape : jurytire3:=convert(J55[rand(7056)],base,2)
     On obtient par exemple : [1,0,1,0,1,0,1,0,1,1,1,1,1,1]
     
   • Le programme jurytire55(J,h) qui se sert de la liste J obtenue précédemment :
     On tape :

     jurytire55(J,h):={
     local k,n,p,la,j,(s:=size(J));
     la:=convert(J[s-1],base,2);
     n:=size(la);
     p:=sum(la);
     k:=iquo(p,2);
     j:=1;
     while (sum(convert(irem(j,2^h),base,2))!=p-k){
     j:=J[rand(s)];
     }
     return j;
     }
     

     On tape : jurytire4:=convert(jurytire55(J,9),base,2)
     On obtient par exemple : [1,1,1,0,1,0,0,0,1,1,1,1,1,0,0,1]
     
4. On peut supposer que la case 0 représente Monsieur Y et que la case n−1 représente Madame X. Donc le jury repésenté par le nombre j est valable si :
   irem(j,2)==0 ou si j<2^(n-1).
   On peut réecrire un programme jury55XY(h,f,p) qui utilise jury55, ou un programme jurys55XY(n,p) qui n’utilise pas jury55 mais jurys, ou utiliser la liste précédente J55 et rejeter les mauvais tirages, ou encore utiliser la liste J du début et rejeter les mauvais tirages.
   • Le programme juryXY55(h,f,p) qui utilise jury55.
     On peut initialiser la liste L soit avec
     L:=makelist(0,1,1); soit avec
     L:=makelist(0,1,comb(h,p-p2)*comb(f-1,p2-1));
     puisque l’on connait sa longueur.

     juryXY55(h,f,p):={
     local LP,L,j,k,l,p2;
     p2:=iquo(p,2);
     LP:=jury55(h,f,p);
     //L:=makelist(0,1,1);
     s:=comb(h,p-p2)*comb(f,p2);
     l:=s-comb(h-1,p-p2-1)*comb(f-1,p2-1);
     L:=makelist(0,1,l);
     l:=0;
     for(j:=0;j<s;j++){
     k:=LP[j];
     if (irem(k,2)==0 or k<2^(h+f-1)) {
     L[l]=<k;
     l:=l+1;
     }
     }
     return L;
     }:;
     

     On tape : JXY55:=juryXY55(9,8,10)
     On a : size(JXY55)=4606
     On tape : jurytire5:=convert(JXY[rand(40606)],base,2)
     On obtient par exemple : [1,0,0,0,0,1,1,1,1,1,1,0,1,1,0,1]
     Mais ce programme appelle le programme jurys précédent....
   • Un programme jurys55XY(n,p) utilise jurys
     On tape le programme jurys55XY(h,f,p).
     On peut initialiser la liste L soit avec
     L:=makelist(0,1,1); soit avec
     L:=makelist(0,1,comb(h,p-p2)*comb(f-1,p2)+
              comb(h-1,p-p2)*comb(f-1,p2-1));
     puisque l’on connait sa longueur.

     jurys55XY(h,f,p):={
     local L,j,k,M,F,l,p2;
     p2:=iquo(p,2);
     L:=makelist(0,1,1);
     //L:=makelist(0,1,comb(h,p-p2)*comb(f-1,p2)+
                   comb(h-1,p-p2)*comb(f-1,p2-1));
     M:=jurys(h,p-p2);
     F:=jurys(f-1,p2)*2^h;
     l:=0;
     for(j:=0;j<comb(h,p-p2);j++){
     for(k:=0;k<comb(f-1,p2);k++){
     L[l]=<M[j]+F[k];
     l:=l+1;
     }
     }
     M:=jurys(h-1,p-p2);
     F:=jurys(f-1,p2-1)*2^h;
     for(j:=0;j<comb(h-1,p-p2);j++){
     for(k:=0;k<comb(f-1,p2-1);k++){
     L[l]=<2*M[j]+F[k]+2^(h+f-1);
     l:=l+1;
     }
     }
     return L
     }:;
     

     On tape : JJXY55:=jurys55XY(9,8,10)
     On a : size(JJXY55)=4606
     On tape : jurytire6:=convert(JJXY55[rand(4606)],base,2)
     On obtient par exemple : [0,0,0,1,1,0,1,1,1,1,1,1,0,1,0,0,1]
     
   • Le programme jurytireXY55(J55) qui se sert de la liste J55 obtenue précédemment (J55:=jury55(h,f,p)) :
     On tape :

     jurytireXY55(J55):={
     local n,k,(s=size(J55));
     n:=size(convert(J55[s-1],base,2));
     k:=1+2^(n-1);
     while (irem(k,2)!=0 and k>=2^(n-1)){
     k:=J55[rand(s)];
     }
     return k;
     }
     

     On tape : jurytire() On obtient par exemple : 63798
     On tape : convert(63798,base,2)
     On obtient : [0,1,1,0,1,1,0,0,1,0,0,1,1,1,1,1]
   • Le programme jurytireXY5(J,h) qui se sert de la liste J obtenue précédemment (J:=jurys(n,p)) :
     On tape :

      jurytireXY5(J,h):={
     local n,k,la,p,(s=size(J));
     la:=convert(J[s-1],base,2);
     n:=size(la);
     p:=sum(la);
     k:=iquo(p,2);
     j:=1;
     while ((sum(convert(irem(j,2^h),base,2))!=p-k) or 
            (irem(j,2)!=0 and j>=2^(n-1))){
     j:=J[rand(s)];
     }
     return j;
     }
     

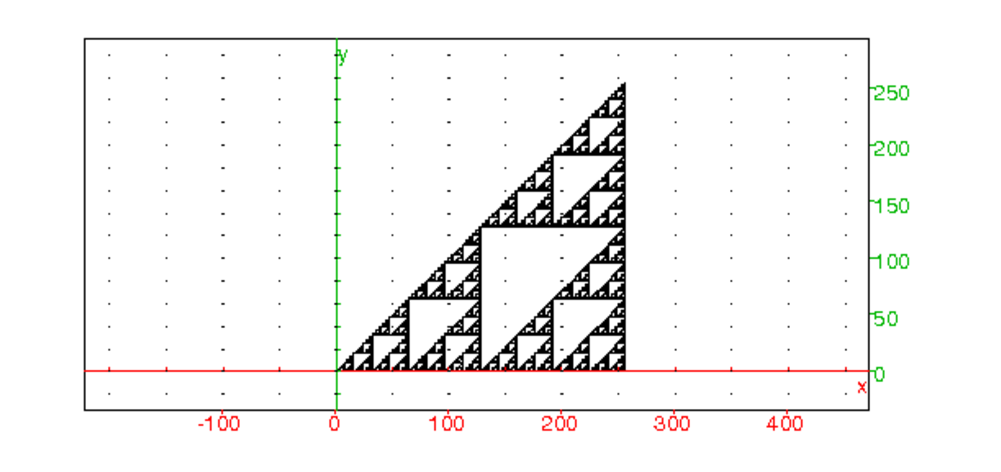
     On tape : jurytireXY5(J,9)
     On obtient par exemple : 24359
     On tape : convert(24359,base,2)
     On obtient : [1,1,1,0,0,1,0,0,1,1,1,1,1,0,1]

9.3  Visualistion des combinaisons modulo 2

9.3.1  L’énoncé

On veut visualiser les points k,j (j≤ k) tel que comb(k,j)=0 mod2

9.3.2  Le programme

On tape :

dessincomb(n):={
  local j,k,L;
  L:=NULL;
  pour j de 1 jusque n faire
    pour k de j jusque n faire
      si irem(comb(k,j),2) alors 
        L:=L,point(k,j,affichage=point_point);
      fsi;
    fpour;
  fpour;
  retourne L;
}:;

On tape :
dessincomb(255)
On obtient :

9.4  Un exercice

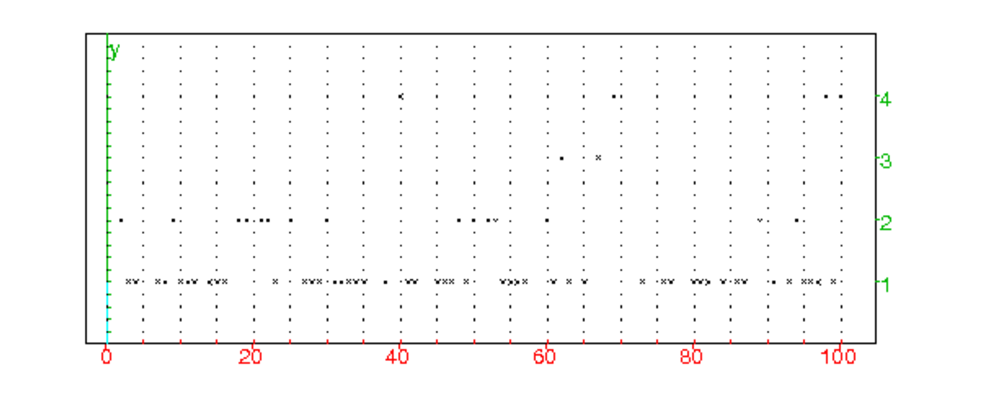
On tire 100 fois de suite au hasard de façon équiprobable un entier p parmi 1,2..100 et on note n_p le nombre de fois où il a été tiré.
Écrire un programme qui représente les points p,n_p On tape :

tirage():={
local p,np,j,L,P;
L:=0$(j=1..100)
pour j de 0 jusque 99 faire
p:=rand(100);
L[p]:=L[p]+1;
fpour;
P:=NULL;
pour p de 0 jusque 99 faire
np:=L[p];
si np!=0 alors P:=P,point(p+1+i*np); fsi; 
fpour;
print(max(L));
retourne P;
}:;

On tape tirage()
On obtient :

9.5  Valeur de e et le hasard

9.5.1  L’énoncé

On tire des nombres au hasard dans [0;1[ et on les ajoute. On s’arrête quand la somme obtenue est strictement plus grande que 1. On peut montrer que le nombres de tirages nécessaires est en moyenne égal à e. Écrire un programme vérifiant expérimentalement ce résultat.

9.5.2  La solution avec Xcas

Dans Xcas, on peut soit utiliser rand(0,1), soit utiliser la fonction f:=rand(0..1) pour obtenir un nombre au hasard entre 0 et 1.
On tape :rand(0.1)
On obtient : 0.482860322576
On tape : f:=rand(0..1)
puis : f() On obtient : 0.8627617261373
puis : f() On obtient : 0.3095522336662 etc....
On écrit le programme :

approxe(n):={
local j,S,k,N;
N:=0;
pour k de 1 jusque n faire
S:=0;
j:=0;
tantque S<=1 faire
S:=S+rand(0,1);
j:=j+1;
ftantque;
N:=N+j;
fpour;
retourne evalf(N/n);
}:;

On tape : approxe(100000)
On obtient : 2.71750000000
alors que evalf(e)=2.71828182846

9.6  Distance moyenne entre de 2 points

9.6.1  L’énoncé

On veut évaluer la distance moyenne entre 2 points choisis au hasard : dans un segment S de longueur 1, dans le carré unité C ou dans le cube unité K.

1. Écrire un programme qui calcule cette distance moyenne lorsque l’on choisit au hasard n fois de suite 2 points dans S,dans C ou dans K, puis généraliser.
2. Faire une représentation graphique permettant de visualiser la répartition des distances dans le cube unité K.

9.6.2  La solution avec Xcas

1. distS(n):={
   local xa,xb,j,d,D;
   D:=0;
   pour j de 1 jusque n faire
   xa:=rand(0,1);
   xb:=rand(0,1);
   d:=abs(xa-xb);
   D:=D+d;
   fpour;
   retourne evalf(D/n);
   }:;
   
   distC(n):={
   local xa,ya,xb,yb,j,d,D;
   D:=0;
   pour j de 1 jusque n faire
   xa:=rand(0,1);ya:=rand(0,1);
   xb:=rand(0,1);yb:=rand(0,1);
   d:=distance([xa,ya],[xb,yb]);
   D:=D+d;
   fpour;
   retourne evalf(D/n);
   }:;
   
   distK(n):={
   local xa,ya,za,xb,yb,zb,j,d,D;
   D:=0;
   pour j de 1 jusque n faire
   xa:=rand(0,1);ya:=rand(0,1);za:=rand(0,1);
   xb:=rand(0,1);yb:=rand(0,1);zb:=rand(0,1);
   d:=distance([xa,ya,za],[xb,yb,zb]);
   D:=D+d;
   fpour;
   retourne evalf(D/n);
   }:;
   
   distp(p,n):={
   local a,b,j,d,D;
   D:=0;
   pour j de 1 jusque n faire
   a:=op(randMat(1,p,0..1));
   b:=op(randMat(1,p,0..1));
   d:=sqrt(sum((a-b)^2));
   D:=D+d;
   fpour;
   retourne evalf(D/n);
   }:;
   
   

   On tape : distS(100000)
   On obtient : 0.333424530881
   On tape : distC(100000)
   On obtient : 0.522140638365
   On tape : distK(100000)
   On obtient : 0.6627691590747
   On tape : distp(4,100000)
   On obtient : 0.777235961163
   On tape : distp(5,100000)
   On obtient : 0.877837288394
   

2. graphdist(n):={
   local xa,ya,za,xb,yb,zb,j,d,L;
   L:=NULL;
   pour j de 1 jusque n faire
   xa:=rand(0,1);ya:=rand(0,1);za:=rand(0,1);
   xb:=rand(0,1);yb:=rand(0,1);zb:=rand(0,1);
   d:=distance([xa,ya,za],[xb,yb,zb]);
   L:=L,point(j+i*d);
   fpour;
   retourne L;
   }:;
   

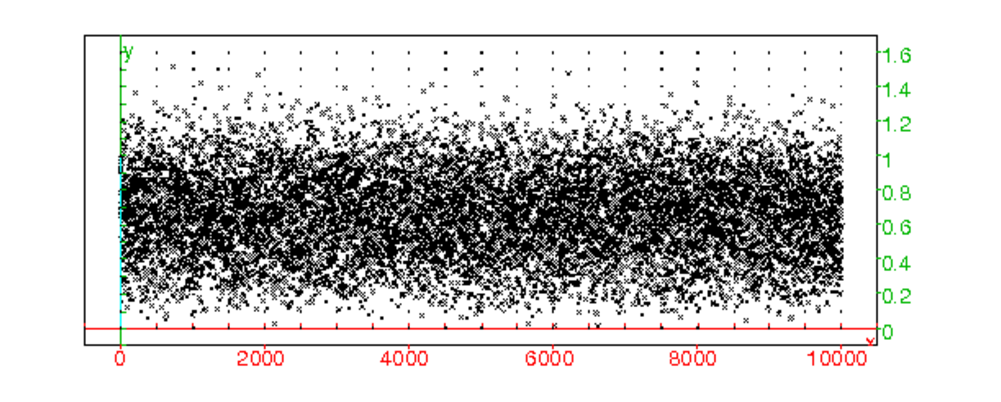
On tape : graphdist(10000)
On obtient :