


Next: Application au calcul de
Up: L'isomorphisme associé à une
Previous: Troisième étape
La géodésique 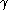 de V est minimale mais elle n'est pas
forcément unique. On va donc modifier V pour rallonger les autres
géodésiques reliant les deux points singuliers de la métrique.
Comme 1-V2 s'annule en P, il existe
de V est minimale mais elle n'est pas
forcément unique. On va donc modifier V pour rallonger les autres
géodésiques reliant les deux points singuliers de la métrique.
Comme 1-V2 s'annule en P, il existe 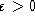 tel
que
tel
que 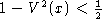 si
si 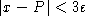 . On modifie
alors V en
. On modifie
alors V en 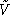 près des autres géodésiques d'Agmon
reliant P et P' en posant
près des autres géodésiques d'Agmon
reliant P et P' en posant 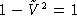 lorsque
lorsque
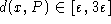 . Ce qui a pour effet
d'allonger la distance de ces géodésiques d'au moins:
. Ce qui a pour effet
d'allonger la distance de ces géodésiques d'au moins:
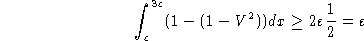
On peut maintenant
assurer que notre géodésique 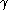 est minimale pour la
distance d'Agmon associée à
est minimale pour la
distance d'Agmon associée à 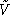 et vérifie la condition
(24).
et vérifie la condition
(24).
Bernard Parisse
Tue Mar 25 14:27:08 MET 1997
![]()
![]() est minimale pour la
distance d'Agmon associée à
est minimale pour la
distance d'Agmon associée à ![]() et vérifie la condition
(24).
et vérifie la condition
(24).