


Next: Correction d'erreurs de transmission:
Up: Arithmétique et exemples d'applications.
Previous: Polynomes
Cryptographie: exemple de la méthode RSA
On se donne 2 nombres premiers 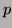 et
et 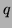 , on pose
, on pose 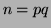 ,
donc
,
donc
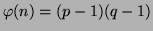 . Soit
. Soit 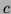 un entier premier avec
un entier premier avec
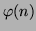 et
et 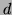 son inverse modulo
son inverse modulo
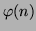 . Alors, pour tout entier
. Alors, pour tout entier
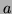 premier avec
premier avec 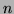 , on a:
, on a:
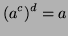
mod
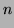
Cette égalité est le principe de base des codages à clefs publiques
(RSA et les logiciels qui l'utilisent comme Pretty Good Privacy,
Gnu Privacy Guard, ssh, etc.). L'entier 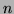 est connu de tout le monde
mais
est connu de tout le monde
mais 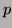 et
et 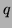 ne le sont pas (si
ne le sont pas (si 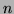 est suffisament grand la
factorisation de
est suffisament grand la
factorisation de 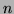 est infaisable en un temps raisonnable), ou
ce qui revient au meme
est infaisable en un temps raisonnable), ou
ce qui revient au meme
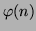 est inconnu. Il est donc impossible
de déduire
est inconnu. Il est donc impossible
de déduire 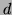 de
de 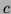 ,
, 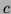 est appelé clef publique de Mr X
et
est appelé clef publique de Mr X
et 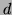 clef secrète de Mr X.
Le codage d'un entier
clef secrète de Mr X.
Le codage d'un entier 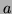 à destination de Mr X uniquement
se fait en envoyant
à destination de Mr X uniquement
se fait en envoyant 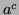 mod
mod 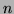 . Seul Mr X peut décoder
. Seul Mr X peut décoder
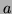 car lui seul connait
car lui seul connait 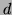 . Mr X peut s'authentifier (signer
un message par exemple) en
envoyant
. Mr X peut s'authentifier (signer
un message par exemple) en
envoyant 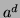 mod
mod 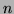 , chacun pourra décoder la signature
, chacun pourra décoder la signature
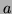 en utilisant la clef publique
en utilisant la clef publique 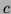 . Pour crypter un message complet,
on commence par transformer ce message en suite d'entiers (premiers
avec
. Pour crypter un message complet,
on commence par transformer ce message en suite d'entiers (premiers
avec 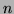 ).
).
Essayez de crypter/décrypter un message de cette manière:
prenez 2 nombres premiers, faites en le produit 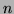 ,
calculer
,
calculer
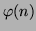 , choisissez une clef publique
, choisissez une clef publique 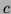 , déduisez
en la clef secrète associée, etc.
, déduisez
en la clef secrète associée, etc.
Remarques:
- L'algorithme RSA est rentré dans le domaine public début septembre
2000 aux États-Unis (contrairement à l'Europe pour l'instant,
les États-Unis autorisent le brevetage de ce type d'algorithmes).
- actuellement on est capable de factoriser des nombres jusqu'à
environ
 (soit environ 400 bits). Les systèmes à clef
publique permettent donc la confidentialité pour des clefs de 512 bits
ou plus. La législation française autorise les clefs de 40 bits
actuellement, un décret devrait faire passer cette limite à 128 bits
très bientot avant une libéralisation plus complète promise par le
premier ministre en janvier 99.
(soit environ 400 bits). Les systèmes à clef
publique permettent donc la confidentialité pour des clefs de 512 bits
ou plus. La législation française autorise les clefs de 40 bits
actuellement, un décret devrait faire passer cette limite à 128 bits
très bientot avant une libéralisation plus complète promise par le
premier ministre en janvier 99.
- le cryptage public avec de grandes clefs peut nécessiter
un temps de calcul trop long, certains logiciels ne l'utilisent que
pour crypter un échange de clef de systèmes de cryptographie
classique (la cryptographie a clef non publique assurant une
confidentialité avec des clefs de taille plus faible ou des
algorithmes plus rapides, par exemple 128 bits).



Next: Correction d'erreurs de transmission:
Up: Arithmétique et exemples d'applications.
Previous: Polynomes
2001-01-19