


Next:
Up: Arithmétique et exemples d'applications.
Previous: Arithmétique et exemples d'applications.
Arithmétique entière.
- La division euclidienne des entiers (comme à l'école primaire): en C
on utilise
% (modulo) et / (quotient euclidient).
Diviseurs d'un entier: 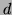 divise
divise 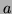 si le reste de
si le reste de 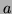 par
par 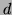 est 0.
est 0.
- Les nombres premiers: ce sont des entiers dont les seuls diviseurs sont
1 et lui-même. Programmation d'un test de primalité trivial.
- PGCD de 2 entiers
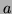 et
et 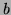 (plus grand diviseur commun de
(plus grand diviseur commun de 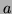 et
et 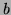 ).
On dit que
).
On dit que 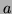 et
et 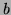 sont premiers entre eux si le PGCD de
sont premiers entre eux si le PGCD de 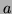 et
et 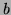 est égal à 1.
Propriété: le PGCD de
est égal à 1.
Propriété: le PGCD de 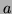 et
et 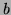 est égal au PGCD de
est égal au PGCD de 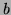 et de
et de 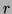 le reste de la division euclidienne de
le reste de la division euclidienne de 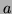 par
par 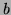 . L'algorithme
d'Euclide consiste à calculer la suite des restes successifs,
le PGCD est le dernier reste non nul.
. L'algorithme
d'Euclide consiste à calculer la suite des restes successifs,
le PGCD est le dernier reste non nul.
Programmer l'algorithme d'Euclide.
- Résolution de l'équation de Bézout: on cherche
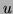 et
et 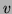 entiers
tels que
entiers
tels que 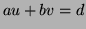 où
où 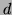 est le PGCD de
est le PGCD de 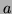 et
et 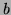 . L'algorithme
est une variante de l'algorithme d'Euclide: on écrit
. L'algorithme
est une variante de l'algorithme d'Euclide: on écrit 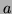 ,
, 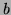 et les
restes successifs comme combinaison linéaire de
et les
restes successifs comme combinaison linéaire de 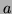 et
et 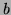 .
.
Notons
![$ [ D \ U \ V ]$](img8.png) pour signifier que
pour signifier que 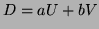 . On a alors
. On a alors
![$ [a \ 1 \ 0]$](img10.png) et
et
![$ [b \ 0 \ 1]$](img11.png) . Si la division euclidienne de
. Si la division euclidienne de 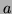 par
par 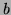 est
est 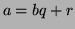 alors
alors 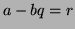 donc la ligne
donc la ligne
![$ [ r \ ? \ ? ]$](img14.png) s'obtient en retranchant
s'obtient en retranchant
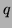 fois la ligne
fois la ligne
![$ [b \ 0 \ 1]$](img11.png) à la ligne
à la ligne
![$ [a \ 1 \ 0]$](img10.png) . On continue
jusqu'à obtenir la ligne
. On continue
jusqu'à obtenir la ligne
![$ [d \ u \ v ]$](img16.png) .
.
Exemple: le pgcd de 25 et 15 est 5. Les deux premières lignes sont
ici
![$ [25 \ 0 \ 1]$](img17.png) et
et
![$ [15 \ 1 \ 0]$](img18.png) .
On a
.
On a
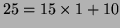 donc
donc 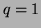 , on retranche
donc à a ligne
, on retranche
donc à a ligne
![$ [25 \ 1 \ 0]$](img21.png) 1 fois la ligne
1 fois la ligne
![$ [15 \ 0 \ 1]$](img22.png) ce qui donne
ce qui donne
![$ [10 \ 1 \ -1]$](img23.png) . Puis on divise 15 par 10:
. Puis on divise 15 par 10:
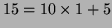 donc
donc 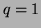 à nouveau et la ligne obtenue est
à nouveau et la ligne obtenue est
![$ [5 \ -1 \ 2]$](img25.png) donc
donc 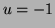 et
et 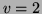 .
.
Programmation de l'algorithme de Bézout.



Next:
Up: Arithmétique et exemples d'applications.
Previous: Arithmétique et exemples d'applications.
2001-01-19