


Next: Cryptographie: exemple de la
Up: Arithmétique et exemples d'applications.
Previous:
Polynomes
On considère ici des polynômes à coefficients entiers ou à
coefficients dans
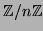 . Certaines des notions d'arithmétique
vues sur les entiers continuent à s'appliquer aux polynômes,
en particulier on peut définir une notion de division euclidienne
selon les puissances décroissantes.
. Certaines des notions d'arithmétique
vues sur les entiers continuent à s'appliquer aux polynômes,
en particulier on peut définir une notion de division euclidienne
selon les puissances décroissantes.
Soit 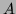 un polynôme non nul,
un polynôme non nul,
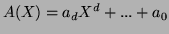 avec
avec 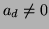 .
L'entier
.
L'entier 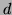 est appelé degré de
est appelé degré de 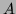 . La division euclidienne de
. La division euclidienne de 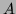 par
par 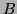 correspond à l'égalité:
correspond à l'égalité:
où le degré de 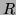 est strictement inférieur au degré de
est strictement inférieur au degré de 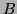 .
Pour calculer
.
Pour calculer 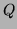 et
et 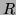 connaissant
connaissant 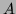 et
et 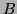 on commence par diviser
le terme de plus haut degré de
on commence par diviser
le terme de plus haut degré de 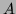 par celui de plus haut degré de
par celui de plus haut degré de 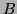 que l'on met comme coefficient de
que l'on met comme coefficient de
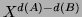 dans
dans 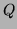 . On multiplie
alors ce terme par
. On multiplie
alors ce terme par 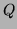 et on le retranche à
et on le retranche à 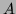 , ce qui diminue le degré
d'un au moins. On recommence tant qu'on peut (tant que le degré est
supérieur ou égal à celui de
, ce qui diminue le degré
d'un au moins. On recommence tant qu'on peut (tant que le degré est
supérieur ou égal à celui de 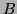 ), losqu'on s'arrête on
obtient le reste.
), losqu'on s'arrête on
obtient le reste.
Programmer la division euclidienne et le PGCD de deux polynômes
dont les coefficients sont dans
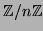 .
.



Next: Cryptographie: exemple de la
Up: Arithmétique et exemples d'applications.
Previous:
2001-01-19
![]() un polynôme non nul,
un polynôme non nul,
![]() avec
avec ![]() .
L'entier
.
L'entier ![]() est appelé degré de
est appelé degré de ![]() . La division euclidienne de
. La division euclidienne de ![]() par
par ![]() correspond à l'égalité:
correspond à l'égalité: