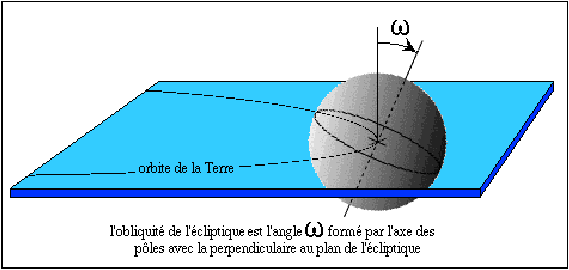
| Figure 1: Saisons et obliquité (source http://www.mnhn.fr/mnhn/lop/DIOGENE/morphologie/orbite.html) |
Mathématiques, climat et énergie.Bernard Parisse |
Résumé: Ce texte reprend certains thèmes des sciences du climat où interviennent des mathématiques au niveau Licence. On abordera la définition des climats, les causes naturelles de variation du climat (influence des paramètres orbitaux de la Terre), et les causes anthropiques (effet de serre).
La température du globe dépend d’une part de l’intensité et de la répartition du rayonnement solaire, d’autre part de la chaleur réémise vers l’espace.
Lorsque le Soleil est à la verticale on reçoit en effet beaucoup plus d’énergie que s’il est bas sur l’horizon. La position du Soleil et la durée de l’ensolleillement journalier dépend d’une part de l’endroit de la Terre où l’on se situe (la latitude: près des poles, des zones tempérées, des tropiques ou de l’équateur), et d’autre part de l’inclinaison de l’axe de rotation de la Terre et de la position de la Terre sur son orbite, responsables des saisons, cf. figure 1.

Figure 1: Saisons et obliquité (source http://www.mnhn.fr/mnhn/lop/DIOGENE/morphologie/orbite.html)
Le calcul de l’inclinaison des rayons du Soleil en fonction de la date et de la latitude fait intervenir principalement de la trigonométrie et un peu de géométrie dans l’espace.
La puissance du rayonnement solaire est inversement proportionnelle à la distance au carré entre la Terre et le Soleil (en admettant que la puissance du Soleil soit constante à la source), la forme de l’orbite de la Terre influe donc sur le climat. Si on néglige les autres planètes et on assimile que la Terre est un point matériel, l’orbite de la Terre est une ellipse (c’est-à-dire un cercle aplati dans une direction) dont le Soleil est un foyer, cf. figure 2.4 Au cours de son orbite la Terre se rapproche ou s’éloigne du Soleil ce qui fait légèrement varier le contraste et la durée des saisons (actuellement les saisons sont moins contrastées dans lhémisphère Nord que Sud et l’hiver boréal est plus court que l’été boréal ce qui explique que février n’ait que 28 jours, plus précisément l’hiver boréal dure 88.99 jours, le printemps 92.75 jours, l’été 93.65 jours, l’automne 89.85 jours). Le calcul précis de la puissance de l’ensolleillement nécessite donc la connaissance d’un peu de géométrie de l’ellipse, ainsi que de la résolution numérique d’équations.
En réalité l’ellipse décrite par la Terre autour du Soleil se déforme au cours du temps, son excentricité varie ainsi que les dates de passage au plus près et au plus loin du Soleil, cf. figure 1 et voir pourquoi en annexe
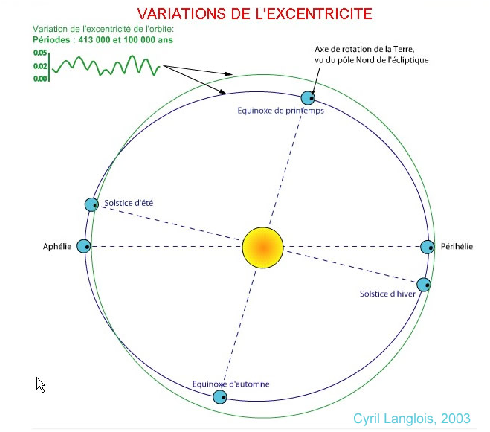
Figure 2: Précession des équinoxes
De plus l’angle d’inclinaison de l’axe de rotation de la Terre varie lentement ce qui répartit l’énergie solaire différemment, plus l’inclinaison est grande plus les poles en reçoivent, cf. figure 1.
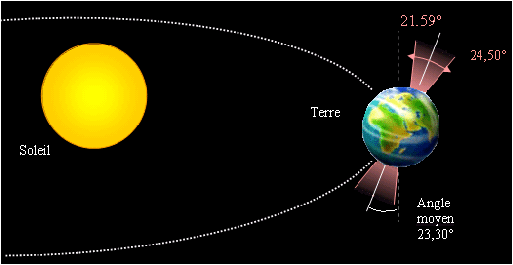
Figure 3: Variation de l’obliquité (source Cyril Langlois)
Ces variations sont à la base de la théorie astronomique des climats de Milankovitch. L’étude numérique des enregistrements du climat du passé sur plusieurs centaines de milliers d’années (en particulier les forages en Antarctique, par exemple Vostok, Dome C, projet Epica) est en bon accord avec cette théorie, on peut ainsi mettre en évidence (par transformée de Fourier) les périodicités principales de ces enregistrements et les comparer avec celles calculées par les astronomes pour l’excentricité, la précession des équinoxes et l’inclinaison de l’axe de rotation de la Terre, cf. figure 1.
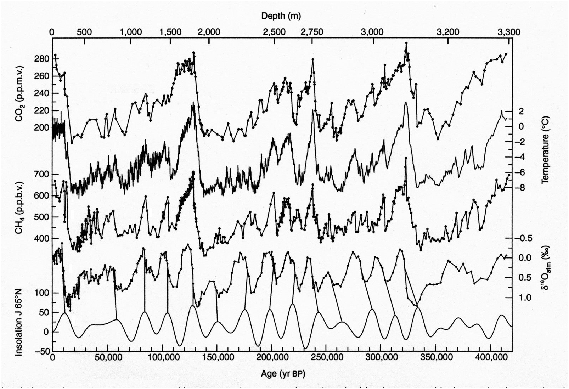
Figure 4: Température et gaz à effet de serre (Vostok)
L’arrivée au sol et la réémission de chaleur par la Terre est elle influencée par les nuages et la présence dans l’air de molécules ayant des fréquences de vibration propres proches de celles du rayonnement émis par le sol (qui peuvent rendre l’air opaque à ce type de rayonnement) provoquant l’effet de serre. Les molécules principalement responsables de l’effet de serre sont le dioxyde de carbone, le méthane, les oxydes d’azote, l’ozone ainsi que les gaz de type halofluorocarbone. Ainsi un doublement de concentration de dioxyde de carbone équivaut à une augmentation d’environ 4 watt par mètre carré au niveau du sol (à comparer aux 1360/4 watt par mètre carré reçu au sommet de l’atmosphère). Leur concentration a varié dans le passé de manière naturelle en phase avec les enregistrement de températures relevés dans les glaces, cf. ci-dessus, on peut le mettre en évidence de manière statistique, ici par une régression linéaire de la température en fonction du CO2, figure 1
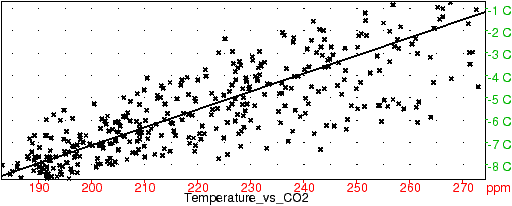
Figure 5: Température en Antarctique et taux de CO2
Depuis le début de l’ère industrielle, cette concentration a beaucoup augmenté, largement au-delà des limites naturelles atteintes au cours des 750 mille dernières années (par exemple 380 parties par million pour le CO2 a Mauna Loa, largement en-dehors de l’intervalle 180-290, en hausse de 2 ppm par an, figure 1)
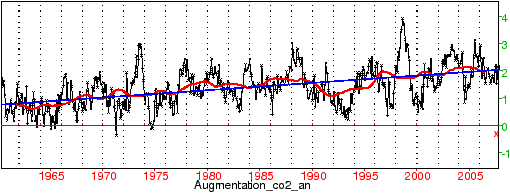
Figure 6: Évolution récente du taux de CO2 (absolue et moyenne mobile de la hausse)
faisant craindre un réchauffement de la planète au 21ème siècle et au cours des siècles suivants, réchauffement trs probablement déjà commencé, figure 1.
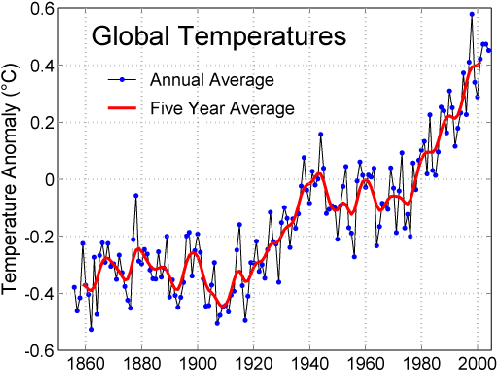
Figure 7: Température actuelle (source IPCC)
La cause principale de l’augmentation de ces concentrations est l’utilisation d’énergie fossiles pour le CO2 (pétrole, gaz naturel et charbon) et d’engrais azotés (agriculture intensive). Une simple règle de trois permet de faire la correspondance
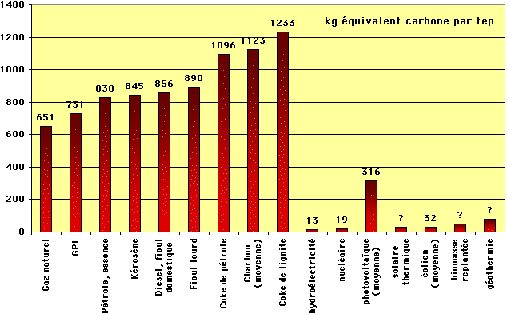
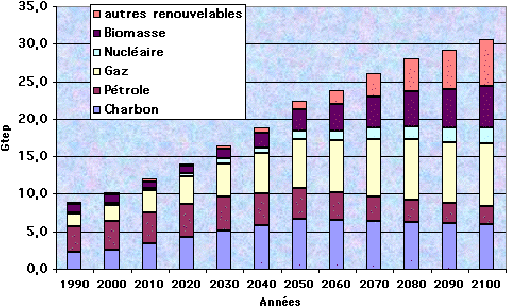
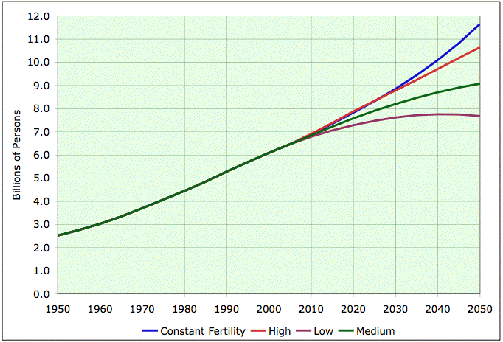
Figure 8: Carbone émis par tonne équivalent pétrole (source J.M. Jancovici) et exemple de scénario énergétique et de population pour le 21ième siècle (IPCC et ONU)
Ainsi, en un an (décembre 2004-novembre 2005), la France a consommé 12.9tonnes équivalent pétrole (tep) de charbon, 95.1 tep de pétrole et 40.5 tep de gaz, dont la combustion a émis dans l’atmosphère 122 millions de tonnes de carbone (sous forme de CO2), soit 1.8 tonne de carbone par habitant, si le reste du monde consommait au même rythme cela correspondrait à 6 parties par millions de CO2 émises par an.
La quantification de l’ampleur du réchauffement (et des autres paramètres climatiques en particulier la répartition et l’intensité des précipitations et des vents) se fait en deux temps, d’une part par des scénari d’emission de gaz à effet de serre, d’autre part par modélisation numérique du climat en fonction des scénari d’émission. La modélisation numérique donne des résultats relativement précis pour la température (3 à 4 degré pour un doublement du CO2), plus incertains pour les précipitations.
Par contre la modélisation des émissions de gaz à effet de serre est beaucoup plus difficile, d’une part parce que les réserves de combustibles fossiles utilisables sont controversées (par exemple sur la date du pic de production pétrolier), d’autre part parce que le mix énergétique du 21ème siècle est largement inconnu (fossile, nucléaire, renouvelables?), mais aussi parce que la réponse de la biosphère au réchauffement est encore mal quantifiée (par exemple on estime que l’océan absorbe actuellement environ la moitié des émissions de CO2, mais la solubilité du gaz carbonique dans l’eau diminue lorsqu’on la réchauffe). Les mathématiques interviennent ici d’abord pour définir le climat (par exemple pourquoi on utilise une série de 30 années pour définir une température moyenne en un lieu donné), dans la réalisation des modèles numériques (nous ne parlerons pas de ce sujet qui dépasse le niveau licence scientifique), dans les modèles statistiques de réchauffement dus aux gaz à effet de serre (corrélation), ainsi que dans les modèles d’émission de gaz à effet de serre, par l’intermédiaire des modèles de production et consommation de combustibles fossiles.
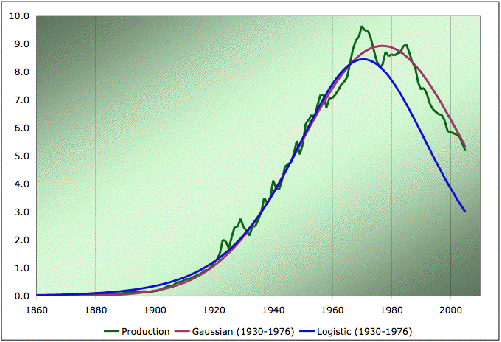
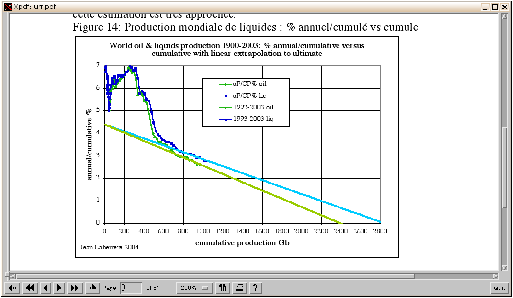
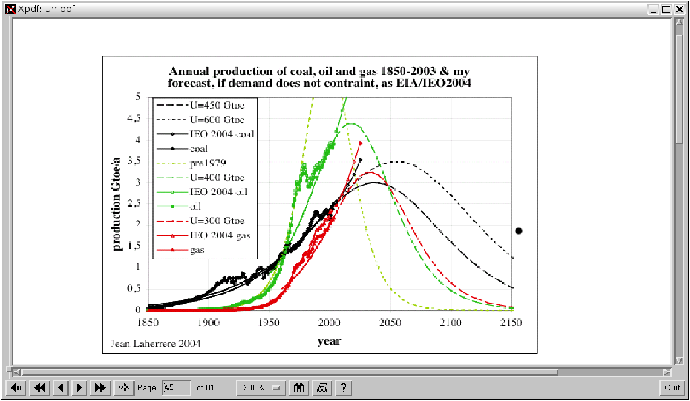
Figure 9: Production de pétrole aux États-Unis (source EIA et Oildrum) mettant en évidence le phénomène de pic pétrolier et recherche du meilleur modèle de prédiction 1976-2004 connaissant l’avant 1976. En millions de barils par jour (1 baril=159 litres). Modélisation des ressources ultimes en pétrole en milliards de barils et de production d’énergie en combustibles fossiles en milliards de tonne équivalent pétrole par an (source Lahérrère)
Pour connaitre la quantité d’énergie recue à un moment
donné, il faut calculer l’angle entre la verticale du lieu
et la direction du Soleil. Plus généralement, on va calculer
les composantes du vecteur Terre-Soleil et les composantes
des vecteurs de la base locale (verticale locale, direction du Sud et
direction du parallèle). On choisit d’abord comme référence
le plan Txy de l’écliptique (plan de l’orbite de la Terre
autour du Soleil), avec Ty orthogonal à l’axe de rotation
de la Terre (donc Tx la projection de l’axe de rotation
de la Terre sur ce plan). Soit θ l’angle que fait la Terre
avec la direction du passage au périhélie, et θ0
l’angle de la position de la Terre au solstice d’hiver avec la
direction du périhélie, l’angle entre la direction Terre-Soleil
et Tx est donc θ−θ0
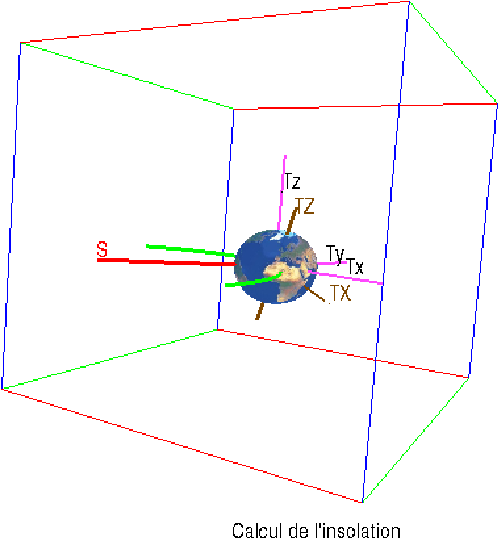
Dans Txyz le vecteur unitaire s
de la direction Terre-Soleil a pour coordonnées :
| s=−(cos(θ−θ0),sin(θ−θ0),0) |
On effectue ensuite une rotation autour de Ty d’angle i l’inclinaison de l’axe de rotation de la Terre. On obtient ainsi un repère TXyZ (TX et TZ se déduisent de Tx et Tz par rotation d’angle i). Dans ce repère le vecteur untaire s a pour coordonnées :
| s=−(cos(θ−θ0)cos(i),sin(θ−θ0), cos(θ−θ0)sin(i)) |
Calculons maintenant dans ce repère TXyZ les coordonnées des vecteurs de la base locale. On se place en un point de latitude l et de longitude φ, on note J la durée d’une période de révolution de la Terre sur elle-même (23 heures 56 minutes, c’est un peu moins d’un jour car il faut encore en moyenne 4 minutes pour compenser le déplacement de la Terre sur son orbite autour du Soleil). La verticale locale a pour coordonnées :
| v=(cos(l)cos(φ+2π t/J),cos(l)sin(φ+2π t/J),sin(l)) |
L’énergie solaire recue au lieu donné (sur une surface horizontale ; pour un panneau solaire, il faudrait calculer les coordonnées d’un vecteur perpendiculaire au panneau) est proportionnelle à
|
où ρ(θ)=a(1−e2)/(1+ecos(θ)) désigne la distance Terre-Soleil. Le calcul de s.v donne, en notant ϕ=φ+2π t/J :
| −s.v = cos(l) cos(ϕ) cos(θ−θ0)cos(i) + cos(l)sin(ϕ) sin(θ−θ0) + sin(l) cos(θ−θ0)sin(i) |
On rassemble les deux premiers termes qui dépendent rapidement du temps par l’intermédiaire de ϕ (le 3ème terme n’en dépend que par θ qui ne varie que d’environ 1 degré pendant une journée) et on applique la formule de trigonométrie:
| A cosα + B sinα = | √ |
| cos(α−α0), | ⎧ ⎪ ⎪ ⎪ ⎪ ⎪ ⎨ ⎪ ⎪ ⎪ ⎪ ⎪ ⎩ |
|
Ici, après avoir factorisé cos(l), on a :
| √ |
| = | √ |
| = | √ |
|
On peut aussi calculer
| tan(α0)= |
| = |
|
qui donne α0 modulo π et compléter en regardant le quadrant où se trouve (A,B), ici α0 et θ−θ0 sont tous deux dans [0,π] ou tous deux dans [−π,0]. Finalement, on obtient le
| (1+ecos(θ))2 s.v |
| s.v = − cos(l) | √ |
| cos(ϕ−ϕ0) − sin(l) cos(θ−θ0)sin(i) |
| tanϕ0 = |
| (1) |
Variations de s.v au cours d’une journée dans l’approximation où
θ ne varie pas :
On obtient une sinusoide entre les deux valeurs extrêmes :
| ± cos(l) | √ |
| − sin(l) cos(θ−θ0)sin(i) |
Le maximum est atteint pour
| ϕ=ϕ0+ π ⇒ 2 π t/J = ϕ0 − φ + π, J=23h56m |
le moment correspondant est appelé culmination (c’est le midi solaire si le maximum est positif) et ne dépend pas de la latitude (bien entendu la valeur du maximum en dépend). Si le maximum est négatif ou nul, la nuit dure 24h. Si le minimum est positif ou nul, le jour dure 24h. Par exemple au solstice d’hiver, θ=θ0, selon la latitude on obtient un maximum négatif pour l=π/2 (pole Nord), positif pour l=−π/2 (pole Sud), le minimum et le maximum croissent entre ces 2 valeurs. Si le maximum est positif et le minimum est négatif, il y a 2 instants ou s.v=0 (lever et coucher du soleil).
L’énergie solaire recue pendant une journée par une surface horizontale est proportionnelle à l’intégrale entre le lever et le coucher de s.v/ρ2. S’il n’y a pas de lever/coucher, soit on ne recoit rien (nuit polaire), soit on recoit l’intégrale entre 0 et 24h de s.v (jour polaire).
L’intervalle entre 2 culminations n’est pas constant au cours de l’année, car ϕ0 n’est pas une fonction linéaire de θ (qui lui même n’est pas linéaire en fonction du temps sauf en première approximation avec une orbite terrestre circulaire). On peut le calculer en dérivant (1). Par exemple dans l’approximation d’une excentricité nulle, au solstice d’hiver (θ=θ0), on obtient
| ϕ0= 0, (1+02) dϕ0 = (1+02) |
|
avec dθ qui correspond à 4 minutes, on trouve dϕ0 correspondant à 4.36 minutes. L’écart entre 2 culminations est donc d’environ 24h 20secondes. Au moment du solstice, le Soleil se lève et se couche donc environ 20 secondes plus tard entre un jour et son lendemain, dans l’hypothèse d’un mouvement circulaire de la Terre autour du Soleil. En réalité, l’orbite terrestre étant faiblement elliptique, l’écart est un peu moins de 30 secondes en hiver et de 15 secondes en été, le mouvement de la Terre autour du Soleil étant plus rapide d’environ 3% au solstice d’hiver et moins rapide d’environ 3% au solstice d’été. Comme 3% de l’écart moyen entre 2 culminations (4 minutes=240 secondes) correspond à 7 secondes cela explique la différence.
Les deux figures (2.2, 2.2) qui suivent représentent la Terre en 4 points de son orbite, les 2 solstices et les 2 équinoxes. Les solstices sont définis par les 2 points de l’orbite où la projection de l’axe de rotation terrestre est parallèle à l’axe Terre-Soleil. Les équinoxes sont définis par les 2 points où il y a perpendicularité.
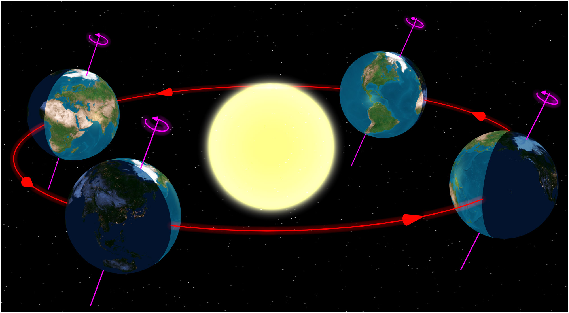
Figure 10: Saisons (hémisphère Nord), source wikipedia
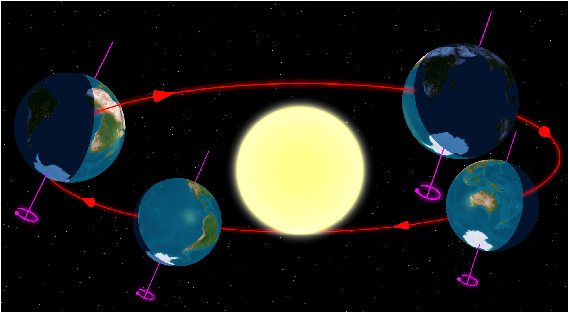
Figure 11: Saisons (hémisphère Sud), source wikipedia
Au solstice d’hiver, on voit que les parallèles situés aux hautes latitudes Nord ne sortent jamais de l’obscurité. Aux latitudes intérmédiaires, le morceau de parallèle situé au jour est nettement plus petit que celui situé dans l’obscurité. À l’équinoxe de printemps, chaque parallèle est à moitié au jour et à moitié dans l’obscurité (derrière la grille). Au printemps, la situtation est analogue. Au solstice d’été, on est dans la situation inverse de l’hiver.
En première approximation, l’orbite de la Terre est uniquement influencée par la force de gravitation entre la Terre et le Soleil, ce dernier pouvant être considéré comme fixe en raison de sa masse (on peut éviter cette approximation en remplaçant le Soleil par le centre de gravité du système Terre-Soleil). La force de gravitation qui dérive d’un potentiel inversement proportionnel à la distance Terre-Soleil est de la forme
| F′= |
| = K |
| , K=−µ<0 |
où r désigne le vecteur Terre-Soleil, mT est la masse de la Terre, µ=GmS est le produit de la constante de gravitation universelle par la masse du Soleil. Le moment cinétique de la rotation de la Terre autour du Soleil est défini par :
| L = r ∧ |
|
On vérifie que sa dérivée est nulle, donc L garde une direction fixe k, orthogonale à r, l’orbite de la Terre reste donc dans le plan défini à un instant donné par l’axe Terre-Soleil et le vecteur vitesse de la Terre. De plus la conservation de L entraine la loi des aires, l’aire balayée par le rayon Soleil-Terre est proportionnelle au temps.
On utilise un repère en coordonnées polaires centré au Soleil, ρ désignant la distance Terre-Soleil et θ l’angle fait par rapport à une direction fixe, on a alors
| L = ρ2 |
| k |
car si on calcule en coordonnées polaires d r/dt, la composante sur le vecteur radial er est dρ/dt, et la composante sur le vecteur perpendiculaire eθ est ρ dθ/dt.
Montrons que le vecteur
| E= |
|
| ∧ L − |
|
est aussi conservé (où on rappelle que µ provient de la force de gravitation F′=F/mT=−µ r/r3). Le deuxième terme est proportionnel au vecteur radial −er, dont la dérivée est le vecteur orthogonal −dθ/dt eθ. Comme L est constant, la dérivée du premier terme est
| F′ ∧ L = |
| ∧ L k = |
| eθ = − |
| ρ2 |
Notons que E est dans le plan de l’orbite, prenons comme origine des angles pour repérer la Terre par rapport au Soleil la direction de E. En faisant le produit scalaire de E avec r, on obtient en notant e la norme de E
|
d’où :
| ρ = |
|
On a les équations de conservation de l’énergie et du moment cinétique :
| + |
| ⎛ ⎜ ⎜ ⎜ ⎜ ⎜ ⎝ | ⎛ ⎜ ⎜ ⎝ |
| ⎞ ⎟ ⎟ ⎠ |
| + | ⎛ ⎜ ⎜ ⎝ | ρ |
| ⎞ ⎟ ⎟ ⎠ |
| ⎞ ⎟ ⎟ ⎟ ⎟ ⎟ ⎠ | =C1, ρ2 |
| = L, K<0, m>0 |
On change de variable dépendante pour ρ, en prenant θ au lieu de t, comme dρ/dt=ρ′ dθ/dt (où ρ′=dρ/dθ), on a :
| + |
| ⎛ ⎜ ⎜ ⎜ ⎜ ⎜ ⎝ | (ρ′2+ρ2) | ⎛ ⎜ ⎜ ⎝ |
| ⎞ ⎟ ⎟ ⎠ |
| ⎞ ⎟ ⎟ ⎟ ⎟ ⎟ ⎠ | = C1 |
On effectue ensuite le changement de variable ρ=1/u, ρ′=−u′/ u2, d’où :
| K u + |
| ⎛ ⎜ ⎜ ⎝ | ⎛ ⎜ ⎜ ⎝ |
| + |
| ⎞ ⎟ ⎟ ⎠ | L2 u4 | ⎞ ⎟ ⎟ ⎠ | = C1 |
soit :
| K u + |
| ( u′2+u2) = C1 |
donc :
| K′ u + u2 + u′2 = C3, K′= |
| <0, C3= |
|
On pose maintenant v=u+K′/2, d’où :
| v2 + v′2 = C3 + |
| = C4 |
On montre (en exprimant v′ en fonction de v puis en séparant les variables), que cette équation différentielle a pour solution générale
| v= | √ |
| cos(θ−θ0) |
D’où :
| ρ = |
| = |
| = |
|
Comme K′<0 et comme la trajectoire de la Terre autour du Soleil passe par tous les angles (donc ρ est défini pour tout θ, le dénominateur ne peut pas s’annuler), on a :
| ρ = |
| , e ∈ [0,1[ |
On définit ensuite a par 2/−K′=a(1−e2), et on obtient finalement l’équation d’une ellipse dont l’origine (le Soleil) est un des foyers :
| ρ = |
|
On suppose maintenant quitte à faire pivoter l’axe des x que θ0=0.
L’orbite de la Terre est donc une ellipse dont le Soleil occupe un des foyers (1ère loi de Képler). On a aussi vu que L=ρ2 dθ/dt est constant, ceci entraine la loi des aires, infinitésimalement on a :
| ρ2 dθ = |
| L dt |
ce qui se traduit par l’aire balayée par le rayon vecteur Soleil-Terre est proportionnelle au temps (2ème loi de Képler). Au cours d’une période T, l’aire parcourue est celle de l’ellipse, donc
| π a2 | √ |
| = |
| LT |
En prenant le carré, et en appliquant
| = a(1−e2) |
on en déduit la troisième loi de Képler :
| 4π2 a3 = µ T2 ⇔ |
| = |
|
où on rappelle que µ est le produit de la constante de gravitation universelle par la masse du Soleil. (On peut évidemment faire le même calcul pour la Lune autour de la Terre).
Définition
L’ellipse E de foyers F1 et F2 de demi-grand axe
a est l’ensemble des points M du plan tels que
| MF1+MF2=2a |
Cf. figure 2.4.
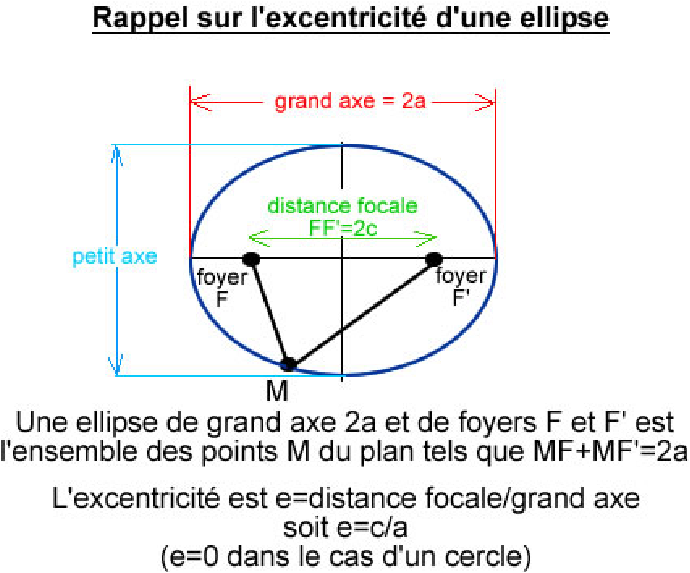
Figure 12: ellipse (source Florence Kalfoun)
On note 2c=F1F2 la distance entre les deux foyers, qui doit être plus petite que 2a pour que l’ellipse soit non vide. L’excentricité de l’ellipse est définie par e=c/a < 1. Si e=0, on obtient un cercle de centre F1=F2 et de rayon a. Si e≠ 0, on va voir qu’il s’agit d’un cercle contracté selon l’axe perpendiculaire à F1F2 dans un rapport de √1−e2. On va également calculer l’équation en coordonnées polaires de E pour montrer que l’équation obtenue ci-dessus est bien celle d’une ellipse dont le Soleil occupe un foyer.
Soit O le milieu de F1 et F2, on se place dans le repère orthonormé dont le premier axe Ox contient F1 et F2 donc les coordonnées de F1 sont (c,0) et celles de F2 sont (−c,0). Soit M(x,y) un point de l’ellipse, on a d’une part :
| MF12 − MF22 = (x−c)2−(x+c)2 = −4cx |
et d’autre part :
| MF12 − MF22 = (MF1 + MF2)(MF1 − MF2 ) = 2a (MF1 − MF2 ) |
donc :
| MF1 − MF2 = |
|
en additionnant avec MF1+MF2=2a et en appliquant c=ea, on en déduit :
| MF1 = a − |
| = a−ex (2) |
En prenant le carré, on a :
| (x−ea)2 + y2 = (a−ex)2 |
d’où :
| y2 + x2 (1−e2) = a2(1−e2) |
finalement :
| x2 + |
| = a2 |
qui est bien la contraction selon Oy de rapport √1−e2 du cercle de centre O et de rayon a (appelé grand cercle de l’ellipse).
En coordonnées polaires, on note ρ la distance de F1 à M, et θ l’angle entre l’axe Ox et F1M. L’abscisse de M est donc :
| x= ea + ρ cos(θ) |
que l’on combine avec (2) pour obtenir :
| ρ = a−ex =a(1−e2) − e ρ cos(θ) |
donc :
| ρ = |
|
ce qui nous permet d’affirmer que l’orbite de la Terre dans l’approximation du point matériel soumis uniquement au Soleil supposé fixe est une ellipse dont le Soleil occupe un foyer.
Il faut prendre garde à ne pas confondre les solstices et équinoxes avec le moment où la Terre coupe le grand axe de son ellipse autour du Soleil. Il n’y a aucune raison que la projection de l’axe de rotation de la Terre sur le plan de l’ellipse soit parallèle ou perpendiculaire au grand axe de l’ellipse, et actuellement ce n’est pas le cas, le solstice d’hiver a lieu le 21 décembre alors que le passage au plus proche du Soleil a lieu vers le 3 janvier (donc pendant l’hiver de l’hémisphère Nord) et le passage au plus loin du Soleil a lieu début juillet (pendant l’été). C’est pour cette raison que les saisons sont moins marquées dans l’hémisphère Nord que dans l’hémisphère Sud. De plus la loi des aires oblige la Terre a se déplacer plus vite lorsqu’elle est proche du Soleil que lorsqu’elle en est éloignée ce qui diminue la durée de l’hiver boréal et augmente la durée de l’été boréal (c’est pour cette raison que février n’a que 28 jours alors que juillet et aout ont 31 jours).
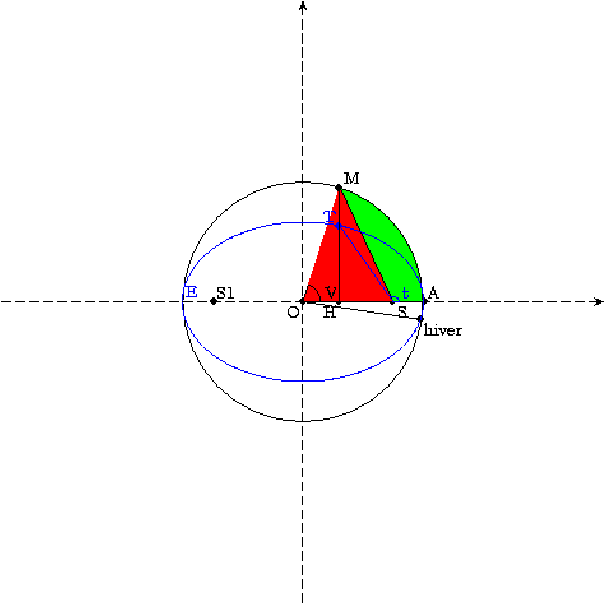
Figure 13: Ellipse et équation du temps
La trajectoire elliptique E de la Terre autour du Soleil est représentée sur la figure 2.6 en bleu, l’excentricité de l’orbite a été énormément exagérée, il s’agit d’une ellipse de foyers S (le Soleil) et S′. Le point A désigne le périhélie de l’orbite (passage de la Terre au plus proche du Soleil), qui a lieu vers le 4 janvier. En noir, on a dessiné le grand cercle de l’ellipse (l’ellipse s’obtient par contraction du grand cercle de rapport √1−e2 où e est l’excentricité de l’orbite). L’aire décrite par le rayon Soleil-Terre (ST) est proportionnelle au temps (loi des aires qui découle de la conservation du moment cinétique), il en est donc de même de l’aire (en vert) du décrite par le rayon SM. Si on ajoute à cette aire verte l’aire en rouge du triangle OSM, on obtient l’aire de l’arc de cercle OAM. Donc
| V × OA2 − |
| OS × HM |
est proportionnel au temps écoulé depuis le passage au périhélie. Comme HM=OM sin(V) et OS= e × OA, on en déduit que
| V − e sin(V) = C t = 2π |
| (3) |
où la constante C s’obtient en faisant varier V de 0 à 2π ce qui correspond à la durée T d’une révolution de la Terre autour du Soleil (1 an).
La relation entre θ (noté t sur la figure) et V s’obtient par exemple en calculant l’abscisse de M
|
Les angles V et θ sont de même signe et
| cos(V) = |
| (4) |
et réciproquement :
| cos(θ)= |
| (5) |
Durée des saisons :
Il suffit de connaitre l’angle θ lors du solstice d’hiver et
de lui ajouter kπ/2 pour k=1,2,3 pour connaitre l’angle θ
au printemps, en été et à l’automne, on en déduit V par (4)
puis le temps écoulé depuis le périhélie avec (3).
Calcul de θ en fonction du temps écoulé depuis le passage
au périhélie :
Il faut calculer V par des méthodes numériques (point fixe ou
méthode de Newton) en appliquant (3), on en déduit
θ avec (5).
En résumé, on a le :
| V − e sin(V) = 2π |
|
| cos(θ)= |
|
La Terre n’est pas une sphère idéale, elle a un renflement au niveau de l’équateur, due à rotation de la Terre sur elle-même (la force centrifuge y est plus importante). Ce renflement est dans un plan qui fait un angle avec le plan de l’écliptique, le Soleil exerce donc un couple sur ce renflement. Ce phénomène est à l’origine de la précession des équinoxes, le passage au périhélie de la Terre se décale dans le temps. De plus, la Terre n’est pas seulement soumise à l’influence du Soleil, mais aussi des autres planètes, en particulier Jupiter. Cela modifie sur de très longues périodes tous les paramètres de l’orbite terrestre, en particulier l’excentricité, la précession des équinoxes, mais aussi l’obliquité (inclinaison de l’axe de rotation terrestre par rapport à la perpendiculaire au plan de l’écliptique). Le calcul de ces variations est bien au-delà des prétentions de ce texte, le lecteur intéressé pourra se référer par exemple aux publications de Laskar (chercher ce mot-clef ou des mots comme orbite, perturbation, symplectique, hamiltonien, ...). On se bornera ici à indiquer que le demi-grand axe ne varie pas, ce qui donne une relation entre les variations de la constante des aires et de l’excentricité
| L est proportionnel à | √ |
|
Les variations des paramètre orbitaux modifient à long terme l’ensolleillement de la Terre (la valeur de l’énergie reçue en un lieu sur une surface horizontale s.v/ρ2 dépend de la latitude, de la position de la Terre sur son orbite mais aussi de l’excentricité de l’orbite, de l’obliquité et de la date du périhélie par rapport aux saisons) et sa répartition sur le globe par latitude, il est naturel de supposer qu’elles influent sur le climat de la Terre. Par exemple, l’énergie moyenne recue par la Terre au cours d’une période T de une année est donnée par
| ∫ |
|
| = |
| ∫ |
|
| = |
|
est proportionnelle à 1/(T L) donc à (1−e2)−1/2 (car T est aussi constant d’après la 3ème loi de Képler). Au premier ordre, la variation de e entraine donc une variation de l’ensolleillement global de
| e2 |
Pour la Terre, cela représente au plus 2.5 pour mille (la période la plus favorable aux glaciations étant celle où l’orbite est circulaire), soit, sans rétroactions, une variation globale de 0.2 degrés Kelvin.
Les carottages de la glace accumulée à Vostok (Antarctique) et ailleurs permettent de reconstituer la température en Antarctique (ou ailleurs) jusqu’à 700 mille ans. On peut effectuer une étude numérique des valeurs obtenues pour faire apparaitre les principales périodicités de ce signal numérique, et comparer avec les périodicités de l’orbite terrestre. On utilisera aussi les données de ces carottes pour mettre en évidence les corrélations entre gaz à effet de serre et température dans le passé.
Soit N un entier fixé. Une suite x périodique de période N est déterminée par le vecteur x=[x0,x1,...xN−1]. La transformée de Fourier discréte (DFT) notée FN fait correspondre à une suite x périodique de période N une autre suite y périodique de période N, définie pour k=0..N−1 par :
| (FN(x))k=yk= |
| xj ωN−k· j, |
où ωN est une racine N-ième primitive de l’unité, on prend ω=e2iπ/N si x est à coefficients réels ou complexes. Cette transformation est linéaire, la transformée de la somme de 2 suites est la somme des transformées, et la transformée du produit par une constante d’une suite est le produit par cette constante de la transformée de la suite.
La transformée de Fourier discréte FN est une transformation bijective dont la réciproque est donnée par :
| FN−1= |
|
| , (FN−1(y))k= |
|
| yjωNk· j |
On le prouve en remplaçant y par sa valeur :
|
Or si ωNk−l=e2iπ(k−l)/N=1 si et seulement si k=l d’où le résultat.
Propriété
La transformée de Fourier discrète d’une suite réelle vérifie
yN−k=yk.
La preuve est immédiate en appliquant la définition.
Un des intérêts de la DFT est de mettre en évidence rapidement d’éventuelles périodicités de x divisant N. Plus précisément soit j est un entier divisant N. Considérons une suite réelle x dont la DFT y est nulle sauf yl et yN−l. Par linéarité, on peut se ramener à 2 cas yl=yN−l=1 et yl=i, yN−l=−i. Dans le premier cas, on obtient xk=ωNlk+ωN−lk=2cos(2π kl/N), dans le deuxième cas, on obtient xk=−2sin(2π kl/N), qui sont périodiques de période N/l.
Réciproquement, si x a comme période T=N/l, alors en posant j=T m + r avec m∈[0,l[ et r∈[0,T−1], on a xj=xr donc :
|
si ωN−kT ≠ 1. Comme (ωN−kT)l=ωN−klT=1, yk=0 si kT=kN/l n’est pas un multiple de N. Finalement si k n’est pas un multiple de l, alors yk=0.
Voyons maintenant le cas de “pseudo-périodes”, supposons donc que x est périodique de période N mais que de plus pour un T>0 quelconque (ne divisant pas forcément N), on ait
| xj+T=xj, ∀ j ∈[0,N−T] |
On peut refaire le raisonnement ci-dessus, modulo des erreurs. plus précisément :
| yk − |
| xj ωN−k· j = |
|
| xr ωN−k (T m+r) |
On calcule donc yk à une erreur de ceil(N/T)T−N termes majorés par |xj| près. Et le membre de droite vaudra :
| xr ωN−kr |
|
Le module de la fraction est égal à
| | |
| | = | |
| | |
il est petit si k n’est pas proche d’un multiple de ceil(N/T). Par exemple, prenons N=216=65536 et T ≈ N/10 =6554. Dans ce cas ceil(N/T)T=10 × 6554=65540, il y a donc une erreur de 4 termes sur le calcul de yk. Si k n’est pas proche d’un multiple de 10, on doit trouver yk proche de 0 relativement à la valeur des |xj|.
Les périodes et pseudo-périodes de x correspondent donc aux valeurs de yk grandes par la règle k * période =N.
Le calcul de la DFT est relativement lent, il nécessite de l’ordre de N2 opérations, car il revient à calculer la valeur du polynôme de degré N−1:
| P(X)= |
| xj Xj |
aux N points 1, ωN, ..., ωNN−1 (on a yk=P(ωNk)). Mais si N est une puissance de 2, on peut calculer de manière plus astucieuse et réduire le nombre d’opérations à un ordre N ln(N). En effet N=2M, on découpe P en 2 parties de même longueur :
| P(x)=xM Q(X) + R(X) |
on a alors
| P(ω2k)= (Q+R) ((ω2)k), P(ω2k+1)= (−Q +R)ω((ω2)k) Sω(x)=∑sk wk xk |
On est donc ramené à deux additions de 2 polynômes de degré M, une multiplication coefficient par puissances (4M opérations), et au calcul des deux DFT de Q+R et R−Q. Si N=2n on vérifie que cela nécessite O(n2n) opérations, donc Nln(N) opérations. On appelle alors FFT cette méthode de calcul (DFT=FFT si N2n).
Les enregistrements ne sont pas faits à des dates régulièrement espacées. Pour se ramener à une suite, il faut interpoler la valeur de la température à une date donnée en fonction de la température aux dates les plus proches de l’échantillon. Le calcul de la FFT de l’écart de température avec la température actuelle sur les 400 000 dernières années donne le graphe figure 3.3
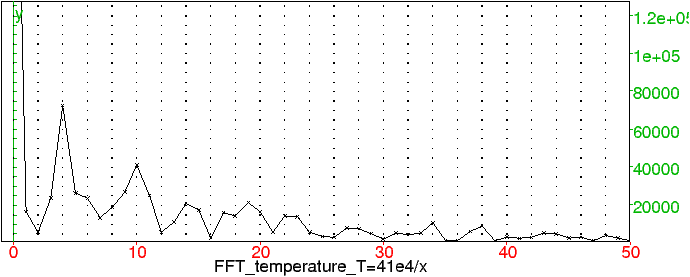
Figure 14: Norme de la FFT de la température de Vostok
On observe que la FFT yk est de module relativement grand pour k=4, k=10 et k proche de 20. La valeur de k=4 correspond à une périodicité de 100 000 ans, celle pour k=10 à 40 000 ans. Il est plus difficile de tirer des conclusions du maximum relatif pour k proche de 20 car 20 est un multiple des périodes précédentes 4 et de 10.
On peut comparer ces 2 périodes tirées de l’enregistrement numérique des périodes de variation des paramètres orbitaux de la Terre :
L’excentricité et l’obliquité ont donc des périodicités que l’on retrouve dans les enregistrements de la température du passé ce qui confirme l’influence supposéee de ces paramètres sur le climat de la Terre.
La figure 3.3 montre la reconstruction par FFT inverse en tronquant la FFT aux 30 premiers entiers (et symétriquement)
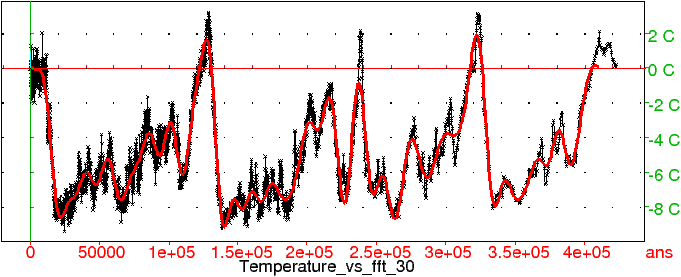
Figure 15: Reconstruction de la température en tronquant la FFT aux 30 premiers entiers
Nous nous sommes intéressés jusqu’à présent à la quantité d’énergie qui arrive du Soleil, sans regarder ce qui peut se passer entre le sommet de l’atmosphère et le sol. Or la composition chimique de l’atmosphère a une influence sur le piégeage des radiations solaires, donc sur le climat. Les molécules des gaz à effet de serre ont des fréquences propres de vibrations qui sont proche des fréquences de radiation émises par la Terre et les rend plus ou moins opaques (alors qu’ils sont quasiment transparents dans le domaine de fréquence des radiations provenant du Soleil). Il s’agit sur Terre principalement du CO2, CH4, des chlorofluorocarbone, de l’ozone (O3) et d’oxydes d’azote. Leur concentration a varié dans le passé, de manière naturelle corrélée avec la température (cf. la section 4.2.2). Elle varie aujourd’hui du fait de l’homme, et les scientifiques élaborent des modèles pour prévoir la réaction du climat à ces variations.
Le domaine des mathématiques concerné sont les probabilités et les statistiques. Il s’agit de savoir quel sens attribuer à une phrase comme “la hausse de température de la Terre au 20ème siècle a été de 0.6 degré”. Il s’agit aussi de savoir pourquoi on considère que 30 ans est un nombre raisonnable d’années pour définir le climat en un lieu donné. On peut faire l’hypothèse que le temps un jour donné n’est pas indépendant de celui du jour précédent (mémoire du temps), mais qu’il est indépendant de celui du même jour l’année précédente : le temps suit une loi qui dépend de la saison. Cette loi subit une lente dérive au cours du temps (variations du climat). Un des résultats importants qui justifie la période de 30 années est le théorème central-limite. Nous allons rappeler quelques définitions avant de l’énoncer.
Lorsqu’on n’est pas capable de prédire de manière déterministe plusieurs événements du même type, on les modélise souvent en disant qu’ils dépendent du hasard mais pas de manière anarchique, ils suivent une loi. Ainsi, le résultat du lancer d’un dé à 6 faces non pipé ne peut pas être prédit, mais en revanche il suit une loi (uniforme), chaque face a autant de chances d’apparaitre qu’une autre. La valeur d’un lancer est une variable aléatoire à valeurs dans {1,2,3,4,5,6} suivant la loi uniforme (la probabilité d’observer chacune des faces de 1 à 6 est de 1/6). Il s’agit ici d’une loi discrète, on ne peut observer que 6 valeurs. L’analogue existe pour une variable aléatoire dont la valeur est réelle (par exemple la température), on utilise alors une densité de probabilité, c’est une fonction f de ℝ à valeurs dans ℝ+ telle que la probabilité d’observer la variable aléatoire dans un intervalle [a,b] soit ∫ab f(x) dx. L’intégrale sur ℝ de f est donc égale à 1. Par exemple pour la loi uniforme sur [1,6], f est constante et vaut 1/5 sur [1,6] et 0 ailleurs. Un autre exemple important est la loi normale développée plus bas.
Lorsqu’on effectue plusieurs observations successives, une observation peut dépendre de l’observation précédente ou non. Par exemple, la température observée un jour donné est en général proche de celle qui sera observée le lendemain. Mais ell est indépendante de celle observée l’année précédente à la même date. De même qu’un jet de dé donne un résultat indépendant du jet de dé précédent. Mathématiquement parlant, l’indépendance se définit par le fait que la probabilité d’observer les événements A et B est le produit des probabilités d’observer A et d’observer B.
Il y a en fait deux notions de moyenne, la première consiste à faire la moyenne d’un échantillon (n observations indépendantes) de la variable aléatoire, la deuxième, appelée espérance de la variable aléatoire, est la moyenne de la valeur de la variable aléatoire pondérée par la probabilité d’observer chacune des valeurs (intuitivement on pense s’en rapprocher lorsqu’on fait la moyenne d’un échantillon assez grand).
|
Le lien entre les deux notions de moyenne est :
| E( |
| ) = E(X) |
L’espérance de la moyenne est égale à la moyenne, lorsqu’on ne connait pas la loi d’une variable aléatoire, on peut estimer son espérance de manière non biaisée par la moyenne de l’échantillon. Intuitivement, si les observations sont indépendantes et plus il y en a, plus la moyenne devrait s’approcher de l’espérance. (on verra avec le théorème central-limite qu’on en sait plus sur la distribution de la moyenne lorsque le nombre d’observations indépendantes pour calculer la moyenne est grand). Pour quantifier cela, il faut pouvoir évaluer l’écart à la moyenne. La moyenne ne donne en effet pas d’informations sur les fluctuations de part et d’autre de la moyenne. Pour cela, on utilise l’écart au carré à la moyenne, dont on fait la moyenne puis on en prend la racine carrée : c’est l’écart-type. On peut calculer l’écart-type pour un échantillon (par rapport à la moyenne de cet échantillon ou par rapport à l’espérance de la loi si elle est connue) et l’écart-type d’une loi (N.B. on appelle variance le carré de l’écart type).
|
On observe que si m est une constante :
| σ2(X−m)=σ2(X) |
C’est faux si m n’est pas constant, on a tout de même la relation
| σ2(X+Y)=σ2(X)+σ2(Y) |
lorsque X et Y sont indépendants.
Contrairement au cas de la moyenne, il y a un ajustement à faire lorsqu’on estime l’écart type d’une loi à partir d’un échantillon si on ne connait pas la moyenne de la loi. En effet, on estime alors la moyenne de la loi à partir de la moyenne de l’échantillon, ce qui conduit à sous-estimer la somme des carrés des écarts à la moyenne. Lorsque les n valeurs de Xi de léchantillon sont indépendants, on a :
| E(σ2 echantillon )= |
| E(σ2(X)) |
En effet :
|
On utilise donc
|
| (Xi− |
| )2 |
au lieu de
|
| (Xi− |
| )2 |
pour estimer l’écart-type d’une loi à partir d’un échantillon.
La définition de ces deux paramètres va nous permettre d’énoncer deux résultats sur la dispersion :
| σ ≠ 0 ⇒ P(|X− |
| | ≥ µ σ) ≤ |
|
| σ2 ≥ |
| (xi− |
| )2 P(X=xi) ≥ µ2 σ2 P(|X− |
| | ≥ µ σ) |
La définition de la loi normale (cf. infra) permet de donner un sens quantitatif au fait qu’une moyenne d’observations indépendantes de même loi tend vers l’espérance de la loi (c’est le théorème central-limite qui sera admis).
Il s’agit d’une loi continue, définie par la fonction
| Nµ,σ2(x)= |
| e |
|
où la constante devant l’exponentielle est déterminée par la condition ∫−∞+∞ Nµ,σ2(x) dx=1.
On montre que la loi normale de paramètres µ et σ2 a pour espérance µ et variance σ2. Pour l’espérance, on fait le changement de variable x=µ +y, on obtient
| E(X) = | ∫ |
| x e |
| = |
| ∫ | (y+µ)e |
| = µ + |
| ∫ | y e |
| = µ |
la dernière égalité provenant de l’imparité de la fonction à intégrer. Pour la variance, il faut faire une intégration par parties pour enlever le terme en x2.
Plage de normalité au niveau de confiance α ∈ ]0,1[: il s’agit d’un intervalle centré autour de la moyenne I=]µ − t σ, µ +t σ[, tel que la probabilité d’être dans I soit de α. Le calcul pratique se fait avec la fonction spéciale erf (error function) définie par
| erf(x)= |
| ∫ |
| e−u2 du |
On montre par un changement de variable que t vérifie l’équation
| erf( |
| )=α |
Ainsi, comme erf(√(2))=0.954..., on utilise souvent la plage de normalité au niveau de confiance de 95% qui est approximativement [µ−2σ,µ+2σ] (la probabilité d’être dans cet intervalle est légèrement supérieure à 95%)
Ce théorème dit que la variable aléatoire obtenue en faisant la moyenne de N variables aléatoires indépendantes et identiquement distribuées (de même loi inconnue) suit une loi gaussienne de moyenne la moyenne de la loi inconnue et d’écart type, l’écart type de la loi inconnue divisé par √N. On estime alors la moyenne de la gaussienne par la moyenne M des observations, et l’écart type S de la gaussienne par l’écart type des observations divisé par √N. Pour une variable aléatoire suivant une loi gaussienne de moyenne m et d’écart type σ, la probabilité de tirer une valeur en-dehors de l’intervalle [m−2σ,m+2σ] est de 5%, on peut estimer que la moyenne “réelle” pour le climat est dans l’intervalle [M−2S/√N,M+2S/√N]. Si S/√N est suffisamment petit, on a une définition raisonnable du climat. Plus N est grand, plus S/√N sera petit, mais d’une part on ne dispose pas de séries de mesure du temps sur des périodes très grandes, d’autre part la loi définissant le climat d’un lieu évolue au cours du temps, on ne peut donc pas prendre N trop grand.
On peut faire le calcul de S/√N pour certaines stations météo (les chiffres sont disponibles gratuitement sur Internet pour de nombreuses stations météo américaines), on trouve pour N=30 des valeurs de l’ordre de 0.1 degré. Lorsqu’on moyenne sur le globe, les écarts-type diminuent au moins d’un ordre de grandeur, ce qui permet de parler de manière raisonnable d’augmentation de température (qui est largement supérieure aux incertitudes dues aux S/√N).
Si deux variables X et Y sont indépendantes, alors
| E(X Y ) = E(X) E(Y) |
Dans le cas général, cette relation n’est pas vraie, on définit la covariance entre X et Y par
| C(X,Y) = E(X Y ) − E(X) E(Y) |
Cette valeur n’est pas “normalisée” (si X et Y ont des unités physiques par exemple ce nombre a une dimension), on définit donc la corrélation par
| c(X,Y) = |
|
ce nombre est sans unité. On montre qu’il appartient à l’intervalle [−1,1]. Si Y=X alors c=1, si Y=−X alors c=−1. Si les variables sont indépendantes, alors c=0. Mais la réciproque est fausse. On utilise toutefois ce calcul pour estimer si deux variables sont corrélées ou indépendantes. Plus précisément, si deux variables paraissent corrélées, on peut essayer d’exprimer l’une en fonction de l’autre, c’est ce qu’on va faire dans la section suivante.
Soit (Xi)1 ≤ i ≤ n et Yi deux séries statistiques. On cherche à savoir s’il est raisonnable de prévoir Yi en fonction de Xi, avec par exemple une relation linéaire Yi = a + b Xi. Pour cela on minimise f(a,b)=∑(a + b Xi −Yi)2 par rapport à a et b, ce qui donne les équations :
| ⎧ ⎪ ⎪ ⎪ ⎨ ⎪ ⎪ ⎪ ⎩ |
|
équivalentes à :
| ⎧ ⎪ ⎪ ⎪ ⎨ ⎪ ⎪ ⎪ ⎩ |
| (6) |
Si on note U la matrice de première colonne remplie de 1, et de deuxième colonne remplie par Xi (en ligne i),
| U= | ⎛ ⎜ ⎜ ⎜ ⎝ |
| ⎞ ⎟ ⎟ ⎟ ⎠ |
et si on note U* la transposée de U,
| U*= | ⎛ ⎜ ⎝ |
| ⎞ ⎟ ⎠ |
on observe que
| U* U = | ⎛ ⎜ ⎜ ⎜ ⎜ ⎜ ⎜ ⎜ ⎝ |
| ⎞ ⎟ ⎟ ⎟ ⎟ ⎟ ⎟ ⎟ ⎠ |
le système (6) devient
| U* U | ⎛ ⎜ ⎝ |
| ⎞ ⎟ ⎠ | = | ⎛ ⎜ ⎜ ⎜ ⎜ ⎜ ⎜ ⎜ ⎝ |
| ⎞ ⎟ ⎟ ⎟ ⎟ ⎟ ⎟ ⎟ ⎠ | = U* Y, où Y= | ⎛ ⎜ ⎜ ⎜ ⎝ |
| ⎞ ⎟ ⎟ ⎟ ⎠ |
Donc la solution est donnée par
| A= | ⎛ ⎜ ⎝ |
| ⎞ ⎟ ⎠ | = inv(U* U) (U* Y) |
En pratique avec Xcas, on place dans un tableur deux colonnes,
une avec les Xi, une avec les Yi, on rajoute une colonne
de 1 avant la colonne des Xi,
on sélectionne les colonnes de 1 et de Xi, on retourne
dans l’historique (hist), on écrit U:= puis on copie
(bouton du milieu de la souris ou touche copie) puis Entrée. On revient
dans mtrw, on sélectionne la colonne des Yi, on repasse dans
hist, on écrit Y:= et on recopie puis Entrée.
On effectue alors A:=inv(tran(U)*U)*(tran(U)*Y).
On peut ensuite juger de la régression en comparant f(a,b)/n
avec la variance de Yi ou en comparant √f(a,b)/n avec
l’écart-type de Yi. On voit que f(a,b)
est la somme des carrés des composantes du vecteur U A − Y,
donc le calcul pratique de f(a.b)/n se fait par la formule
l2norm(U*A-Y)^2/size(Y), à comparer avec stddev(Y)^2.
Plus ce rapport est proche de 0, plus on explique les variations de Yi par
la régression linéaire.
On peut montrer que les coefficients de la droite sont donnés par :
| b= |
| , a = |
| − b |
|
et
| f(a,b) = n (1−r2) σ(Y)2, r= |
|
On montre que cette méthode se généralise (dans sa formulation matricielle), si on veut prévoir par exemple Yi à partir de deux séries statistiques xi et Xi avec une relation linéaire de la forme Yi=a+bxi+cXi, alors (a,b,c) est obtenu en calculant inv(U* U) U* Y, où cette fois la matrice U possède 3 colonnes, la colonne de 1, la colonne des xi et la colonne des Xi. Les calculs pratiques se font de manière identique.
On peut aussi supposer que Y dépend de manière non linéaire de X, par exemple logarithmique, exponentielle, polynomiale, etc. mais toujours de manière linéaire des paramètres à déterminer et calculer ces paramètres en utilisant la même méthode (minimiser l’erreur quadratique). Ceci peut servir par exemple à modéliser la consommation d’une denrée non renouvelable (par exemple les combustibles fossiles) par une fonction logistique ou par une gaussienne.
Si on fait une corrélation température-CO2 sur les 400 000 dernières années, on trouve un rapport f(a,b)/n sur variance de 0.35, soit une qualité de corrélation de 0.65 (65% de la variance de la température est expliquée par le taux de CO2) et un coefficient d’augmentation de température de 9 degrés pour 100 ppm de CO2. On peut aussi faire une corrélation température en fonction du CO2 et du CH4, on trouve alors 6 degrés pour 100 ppmv de CO2 et 1.5 degré pour 100 ppbv de CH4 avec une qualité de corrélation de 0.68.
Bien entendu, une corrélation statistique ne suffit pas à conclure qu’une des variables dépend (au moins partiellement) de l’autre, mais ici la physique nous montre que l’augmentation du taux de CO2 augmente les radiations solaires capturées au niveau du sol, la corrélation permet de quantifier cet effet (calcul que l’on pourra comparer à celui obtenu par d’autres méthodes).
Dans cette section, on présente différents types de modèles mathématiques qui idéalisent la situation réelle. Les principaux types s’appliquant ici sont les modèles discrets, les modèles continus se ramenant à des équations ou systèmes différentiels et les modèles de type équations aux dérivées partielles (qui ne seront pas présentés ici).
On suppose ici que la Terre est assimilable à un océan (pas de glace modifiant l’albédo) recevant un rayonnement solaire constant et émettant un rayonnement dont la puissance est composée d’une partie proportionnelle à T4 (comme un corps noir) dont on retranche le piégage du au gaz carbonique (proportionnel au log de la concentration de CO2). La différence entre les deux rayonnements incident et renvoyés sert à réchauffer l’eau. On obtient l’équation (où le coefficient 6 et le ln pour le taux de CO2 proviennent de calculs de physique)
| = k ( 6 ln(CO2/280) − σ (T4−T04) ) |
Le calcul de k donne (86400 × 365)/(3e6 × 4.18e3) =0.0025 degrés par an (on chauffe l’eau sur 3000 mètres en moyenne avec une puissance de 1W/m2). On peut prendre T0=288 (15 degré celsius), et pour σ la constante de Stefan-Boltzman (5.67e−8, ceci aura tendance à sous-estimer le phénomène car l’eau de mer n’est quand même pas un corps noir). On peut prendre par exemple une variation du taux de CO2 constante et égale à 2 ppm par an, soit si t est exprimée en années
| CO2=380+2(t−2005) |
On ne sait pas résoudre exactement ce type d’équation différentielle, on utilise alors des méthodes de résolution approchée. La plus simple consisterait dans notre cas à supposer la température du globe constante pendant une année et à calculer la différence entre l’année en cours et l’année suivante
| T(t+1)=T(t) + k ( 6 ln(CO2/280) − σ (T4−T04) ) (7) |
Il s’agit de la méthode d’Euler (avec un pas de 1 an), graphiquement cela revient à tracer le graphe de la solution d’une équation différentielle en suivant les tangentes.
L’avantage de cette discrétisation est qu’on peut modéliser de manière plus réaliste la variation du taux de CO2.
L’homme émet dans l’atmosphère des gaz à effet de serre principalement par combustion des pétrole, gaz, charbon, également par la déforestation et les émissions de méthane de l’agriculture. Un petit calcul élémentaire permet d’établir la correspondance entre 1 ppm de CO2 (une partie de CO2 par million en volume) et 2 Gt (gigatonnes) de carbone.
Le mètre a été pendant longtemps défini comme 1/40 millionième de la circonférence de la Terre, on a donc 2π R=4e7 m où R désigne le rayon de la Terre. On en déduit la surface de la Terre
| 4 π R2= (4e7)2/π=5e14 m2 |
La pression de l’air au sol est équivalente à une colonne d’eau de 10m (ou encore 76cm de mercure dont la densité est 13). La masse de l’atmosphère terrestre est donc égale à celle de 5e15m3 d’eau soit 5e18kg. L’air est pour trois quarts composé d’azote (N2 masse molaire 214=28), et pour le reste d’oxygène (O2 masse molaire 216=32), alors que le carbone C a une masse molaire de 12. Comme il y a 1 atome de carbone par molécule de CO2, on en déduit que la masse de carbone correspondant à une concentration de 1ppm de CO2 est de :
| * 5e18 * 1e−6= 2.1 e12 kg |
soit 2.1Gt de carbone.
La consommation mondiale de combustibles fossiles s’établit pour 2003 à 3.5 Gtep (giga-tonne équivalent pétrole) de pétrole, 2.3 Gtep de gaz naturel et 2.4 Gtep de charbon. Avec un taux moyen en tonne de carbone par tep de 0.856 pour le pétrole, 0.651 pour le gaz et 1.123 pour le charbon, on a émis
| 3.5 × 0.856 + 2.3 × 0.651 + 1.123 × 2.4 = 7.1 Gt C |
ce qui correspond à 3.5 ppm de carbone. Auquel il faut ajouter le carbone émis par déforestation, retrancher le CO2 absorbé par l’océan et les écosystèmes, on a mesuré une augmentation de 2ppm.
Les incertitudes sur la sensibilité du climat à une augmentation fixée des taux de gaz à effet de serre sont assez faibles. Par contre les prévisions de taux de gaz à effet de serre sont très incertaines puisque par exemple la concentration de CO2 à la fin du siècle dépend de la quantité de combustibles fossiles que nous aurons brulée. Celle-ci est très incertaine, car :
Plusieurs modèles existent donc, par exemple les scénarios du GIEC ou d’experts (par exemple ceux dérivés des projections de l’ASPO). Quelques principes mathématiques sous-tendent ces modèles :
Les modèles les plus utilisés sont les suites arithmétiques, les suites géométriques, et plus générallement les suites récurrentes. Historiquement, c’est Malthus qui soutint la thèse que la production croit comme une suite arithmétique, alors que la population croit comme une suite géométrique, prédisant de gros problèmes lorsque la suite géométrique dépassait la suite arithmétique. C’est Verhulst qui proposa alors le modèle logistique pour améliorer la modélisation (cf. infra dans le cas continu).
Plus générallement, les suites récurrentes un+1=f(un) permettent de modéliser des phénomènes où la relation ne dépend pas explicitement du temps, il est alors intéressant d’étudier les positions d’équilibre aussi appelés points fixes, et leur stabilité (si u0 est proche d’un point fixe l, la suite un converge-t-elle vers l ?). On peut aussi étudier la sensibilité de l’équilibre à une variation des paramètres définissant la fonction f (déplacement de l’équilibre, passage d’un équilibre stable à un équilibre instable). Le résultat principal sur la stabilité est que si |f′(l)|<1 alors l’équilibre est stable (on peut le comprendre intuitivement en faisant une représentation graphique de la suite en dimension 1).
Si f dépend explicitement du temps (i.e. de n), par exemple pour (7), il n’y a pas de résultats simples. On peut résoudre explicitement quelques cas particuliers, par exemple un+1=Aun+P(n), où A est une matrice constante et P un polynôme.
On a vu dans les sections précédentes que de nombreux modèles se ramenent à la résolution d’équations différentielles ou de systèmes différentiels :
| = F(X(t),t) |
où X est la quantité recherchée et t le temps. La plupart du temps ces équations et systèmes ne peuvent être résolues que de manière numérique, mais certains cas particuliers importants peuvent être résolus exactement. Nous verrons le cas du modèle logistique comme exemple d’équation résoluble (qui est utilisé comme modèle de production d’énergie non renouvelable) et les systèmes différentiels affines (qui aident à comprendre une amélioration du modèle très simple, 5.1, tenant compte des interactions entre température, CO2 et albédo). Pour les cas non résolubles, on essaie de déterminer le comportement qualitatif de l’équation à partir de cas connus, en général en linéarisant. On mettra en évidence sur ces systèmes la notion d’équilibre stable et instable, et la notion de rétroaction.
Le modèle exponentiel, historiquement proposé par Malthus et encore très (trop?) utilisé par les économistes, correspond à l’équation différentielle :
| = b |
où y(t) désigne la quantité totale extraite au temps t. La solution de cette équation est une exponentielle qui tend vers +∞ lorsque t tend vers l’infini, ce qui n’est pas possible pour une ressource non renouvelable. Pour avoir un modèle plus réaliste qui tienne compte d’une ressource finie, Verhulst (1840) passe d’un taux d’accroissement constant à un taux linéaire et qui diminue lorsque y augmente
| = −ay+b =−a(y−c), a>0, c= |
|
La solution de cette équation est appelée fonction logistique. On sépare les variables :
| dt=− |
|
on décompose en éléments simples :
| a dt = |
| ⎛ ⎜ ⎜ ⎝ |
| − |
| ⎞ ⎟ ⎟ ⎠ |
soit :
| b dt = | ⎛ ⎜ ⎜ ⎝ |
| − |
| ⎞ ⎟ ⎟ ⎠ |
d’où en intégrant :
| bt+C= ln(| |
| |) |
puis, en enlevant les valeurs absolues et en posant K=± eC :
| =Kebt ⇒ y(1+Kebt)=Kcebt |
Donc K>0, on peut poser K=e−bt0 et finalement :
| y = c |
| =c |
|
On peut étudier le comportement de la fonction y en fonction du temps, en t=−∞, la limite de y est nulle, la fonction croit pour t négatif comme une exponentielle
| y ≈t → −∞ c eb(t−t0) |
(avec le même taux de croissance que lorsque a=0) et est convexe. Pour t=t0, y=c/2, la fonction a un point d’inflexion et devient concave pour rejoindre sa limite c en t=+∞. Si on calcule y′ qui modélise la production instantannée, on obtient :
| y′ = bc |
| = |
|
On observe que y′ a un graphe en forme de cloche avec deux limites
nulles aux extrémités et un maximum en t=t0 :
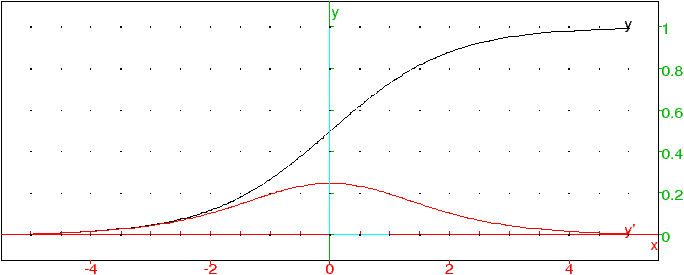
En pratique, pour modéliser y on effectue une régression linéaire du quotient de la production annuelle par la production cumulée (par exemple pour le pétrole depuis 1900) en ordonnée (ce qui représente dy/ydt) en fonction du temps. Un grand intérêt de ce modèle est qu’il permet de prédire la quantité totale que l’on pourra extraire. Sa principale faiblesse est la sensibilité de cette estimation en fonction de la qualité des données initiales et des irrégularités (par exemple chocs pétroliers). Pour la production de pétrole, on peut un peu l’améliorer en modélisant plusieurs cycles de pétrole donc en additionnant plusieurs courbes logisitiques (pétrole on-shore facile, pétrole offshore, deepwater, ultra-deepwater, polaire, pétroles lourds).
On s’intéresse plus générallement à des systèmes affines:
| =AX+C (8) |
où X(t)=(x1,...,xn) est un vecteur de dimension n, A une matrice n,n et C=(c1,...,cn) est un vecteur constant Plus générallement, on peut résoudre exactement ce type de système lorsque C ne dépend que du temps.
Pour les systèmes qui nous intéressent, on suppose en géneral que les coefficients sur la diagonale sont négatifs, de sorte que si les interactions entre paramètres étaient nulles, la solution du système convergerait. Pour une modélisation réaliste, A n’est pas diagonale, les coefficients non diagonaux traduisent des rétroactions entre les paramètres, ces rétroactions peuvent être positives si ces coefficients sont positifs (l’interaction amplifie l’action de la variation originale du paramètre) ou négatives dans le cas contraire.
Si la matrice A est inversible, il existe une unique position d’équilibre, en effet si dX/dt=0, on a X=Xe=−A−1 C et réciproquement cette valeur de X est solution de (8). Pour une condition initiale X0 quelconque, on peut alors se demander si X(t) va se rapprocher de la position d’équilibre Xe (équilibre stable) ou non (instabilité si on s’éloigne de l’équilibre). Si le système est stable, on peut aussi se demander comment la position d’équilibre varie lorsque C varie (par exemple pour les paramètres du climat si le forçage radiatif est modifié par variation des paramètres orbitaux de la Terre).
Il ne faut pas confondre la question de la stabilité du système et l’existence de rétroactions positives ou négatives. Un système avec des rétroactions positives peut très bien être stable.
On se limitera ici au cas de matrices A réelles et diagonalisables (sur ℂ). Soient λ1,...,λn les valeurs propres de A (réelles ou par paires de complexes conjugués) et P la matrice de passage vers une base propre correspondante
| P−1 A P=D = diag(λ1,...,λn) |
On pose X=PY (Y=P−1X), on a alors
| =P−1 |
| = P−1(AX+C) = P−1APY + P−1C = D Y + P−1C |
Soit B=P−1C, on est ainsi ramené à n équations différentielles linéaires d’ordre 1 à coefficients constants :
| = λk yk + bk |
Lorsque bk=0, l’équation admet pour solution générale
| yk(t)= c eλkt |
En faisant varier la constante c=c(t), et en remplaçant dans l’équation vérifiée par yk, on obtient :
| c′ eλkt = bk ⇒ c′ = e−λkt bk |
donc c=∫e−λkt bk, et si bk est constant,
| c(t)=− |
| e−λkt + K |
où la valeur de K se calcule en posant t=0, finalement la solution est donnée par :
| yk(t)=−bk/λk + (yk(0)+ |
| ) e−λkt |
c’est la somme d’un terme constant (k-ième coordonnée de la position d’équilibre dans la base propre) et d’un multiple d’une exponentielle dont le comportement lorsque t tend vers +∞ permet de déterminer si le système est stable.
Si ℜ(λk)>0 pour au moins une des valeurs de k, alors la composante correspondante yk(t) tend vers l’infini, et le système est instable. Si ℜ(λk)=0, la composante reste bornée, il n’y a pas convergence vers l’équilibre mais le système fait des tours autour de la position d’équilibre. Si ℜ(λk)<0 pour toutes les valeurs de k, il y a convergence (exponentiellement rapide) vers l’état d’équilibre, le système est stable, la vitesse de convergence est caractérisée par l’inverse de la valeur propre dont la partie réelle est la plus proche de 0.
On prend souvent comme exemple de cette théorie le modèle proie-prédateur, on peut ici dans le contexte énergétique proposer un modèle baril (prix)-demande-production (sans contrainte géologique). Plus le prix du baril est élevé, plus la production augmente et la demande baisse. Plus la production est élevée, plus le baril baisse. Plus la demande est élevée, plus le baril monte. On est donc en dimension 3.
| ⎛ ⎜ ⎜ ⎝ |
| ⎞ ⎟ ⎟ ⎠ | = | ⎛ ⎜ ⎜ ⎝ |
| ⎞ ⎟ ⎟ ⎠ | ⎛ ⎜ ⎜ ⎝ |
| ⎞ ⎟ ⎟ ⎠ | + C |
On remarque que 0 est valeur propre, la trace de la matrice est nulle, il y a 2 valeurs propres imaginaires pures ± i √bd+ac conjuguées et le système va effectuer des cycles (dont la période est 2π/√bd+ac).
Un système différentiel général d’ordre 1 peut s’écrire
| = F(X(t),t) |
Si F ne dépend pas explicitement du temps (systèréme autonome), on peut commencer par chercher les positions d’équilibre possibles, i.e. les solutions de F(X)=0, puis si Xe est une solution, linéariser, c’est-à-dire résoudre
| = F′(Xe) (X−Xe) |
pour voir si en partant de conditions initiales proches de l’équilibre, le système s’en approche (stable) ou s’en éloigne (instable).
Un autre cas est intéressant, celui d’une perturbation dépendant du temps
| F(X(t),t)=G(X)+p(t) |
par exemple pour étudier la perturbation introduite par l’ajout de CO2 à un système linéaire modélisant le système climatique non perturbé. Dans le cas du CO2, on peut par exemple supposer un taux d’émission constant (p(t)=p) et voir comment l’équilibre du système climatique est affecté. Plus générallement, pour trouver l’équilibre on souhaitera trouver Xe(t) tel que
| G(Xe(t))+p(t)=0 |
c’est le théorème des fonctions implicites qui permet de déterminer Xe(t) en fonction de t, sous réserve que ∂X G soit inversible. Si le système différentiel linéarisé correspondant à G(Xe(t)) est stable et que la perturbation p(t) varie lentement par rapport aux constante de temps caractérisant la stabilité ou est d’amplitude faible, alors la position d’équilibre va suivre. Pour le système climatique soumis aux variations externes des paramètres orbitaux, on peut considérer que c’est le cas. Par contre ce n’est pas vrai pour la perturbation anthropique du CO2, on peut toutefois étudier le système linéarisé, en supposant que G′(Xe) reste à peu près constant.
On considère 3 paramètres pour modéliser le climat, la température moyenne T, la masse de glace G (qu’on suppose relié à l’albédo par la surface de glace) et le taux de CO2 dans l’air C. La température moyenne influe sur la puissance rayonnée (proportionnelle à T4), sur le CO2 dissous dans l’océan (si T augmente, C augmente) et sur la glace (si T augmente, G diminue). Le CO2 influe sur la puissance rayonnée en fonction de −ln(C) et sur le taux de CO2 dissous dans l’eau de mer. La glace influe sur la puissance rayonnée, en fonction de la surface qu’on peut modéliser par G(2/3). Enfin la puissance rayonnée est reliée à la température par la capacité calorifique de l’océan.
Il y a évidemment encore beaucoup de simplifications dans un tel modèle à 3 paramètres, la température de l’océan n’est pas homogène et la température des eaux profondes ne varie que très lentement, il y a d’autres gaz à effet de serre, ...
On a alors
| ⎛ ⎜ ⎜ ⎝ |
| ⎞ ⎟ ⎟ ⎠ | = F = | ⎛ ⎜ ⎜ ⎝ |
| ⎞ ⎟ ⎟ ⎠ |
où cc est proportionnel la capacité calorifique de l’océan, f est une fonction décroissante, ∂T g est positif.
On peut aussi utiliser ce type de modéle pour obtenir le pourcentage de CO2 émis par l’homme restant dans l’atmosphère au bout de t années
| CO2(t)=18+26 e−t/3.4 + 24 e−t/21 + 18 e−t/70 + 14 e−t/420 |
Les fluides de l’atmosphère obéissent aux équations physique de la dynamique des fluides. Contrairement au problème à 2 corps, on ne peut pas résoudre ces équations de manière exacte. On utilise alors des méthodes numériques, en discrétisant l’état de l’atmosphère. On obtient alors une solution approchée des équations, c’est le principe des prévisions numériques météorologiques. Ce principe s’applique aussi au climat. On peut s’étonner que le même principe qui ne permet pas des prévision fiables à plus de quelques jours puisse permettre de faire des prévisions à l’échéance du siècle. La contradiction n’est qu’apparente, parce que les modèles ne prévoient pas le temps précis un jour donné, mais le temps moyen, en fonction des grandes contraintes énergétiques (ensoleillement, effet de serre) de même qu’on peut prévoir qu’il fera en moyenne plus chaud en été qu’en hiver parce que l’ensoleillement est plus important en été qu’en hiver. L’intérêt des modèles est de pouvoir quantifier le “il fera plus chaud si l’effet de serre est renforcé”.
Les problèmes mathématiques liés à la modélisation du climat sont liés à la stabilité des méthodes de résolution numérique. On peut en avoir une petite idée en étudiant les méthodes numériques d’intégration ou la méthode d’Euler pour résoudre des équations différentielles de type y′=f(x,y) (mais ici on a 3 dimensions d’espace et 1 de temps et beaucoup plus qu’une variable, il y a la pression, la température, l’humidité, ...). On peut aussi s’inspirer d’exemple de suites itératives pour essayer de comprendre certains phénomènes.
Le calcul du rendement d’un panneau solaire thermique découle du calcul de l’ensolleillement fait au théorème 1, mais il faut tenir compte du fait que la normale n au panneau solaire n’est plus la verticale locale. On exprime les coordonnées de n dans le repère local orthonormé formé de la verticale locale, du Sud local, et de la direction obtenue par produit vectoriel des deux vecteurs précédents. La verticale locale v est connue (cf. section 2.1), le vecteur normé porté par la direction du Sud local est égal à l’opposé de la dérivée de v par rapport à la latitude, après normalisation.
Lorsque l’angle avec la verticale est fixé, on a bien sur intérêt à aligner le panneau avec le Sud local. On peut calculer l’angle optimal pour recevoir le maximum d’énergie solaire tout au long de l’année, mais il est plus intéressant de calculer l’angle optimal pour maximiser le rayonnement reçu pendant la période de chauffe pour minimiser l’utilisation d’un appoint (par exemple sur la période automne-hiver, on trouve un angle voisin de 60 degrés à nos latitudes sans tenir compte de la météo). On peut aussi chercher à optimiser l’angle au solstice d’hiver si on souhaite éviter l’utilisation d’un appoint (on utilisera par contre plus de surface de panneaux, ceux-ci devant alors être toujours excédentaires).
Il s’agit de générer de la chaleur (four solaire) ou du courant électrique comme avec une centrale thermique classique, la chaleur étant fournie par les rayons solaires au lieu de la combustion de charbon, gaz ou fuel. Les rayons solaires ne sont bien sur pas suffisamment chauds pour obtenir une chaleur ou un rendement suffisant sans concentration. La concentration se fait à partir d’un ou de miroirs qui réfléchissent les rayons en une zone la plus petite possible.
Etude idéalisée : on suppose que le miroir peut prendre la forme d’une courbe régulière (ou que les miroirs sont suffisament petits pour être assimilable à des tangentes à une courbe). Quelle forme doit prendre la courbe pour focaliser les rayons solaires incidents en un seul point ? Une réponse est connue depuis longtemps, il s’agit d’une parabole (ou plus précisément d’un paraboloide de révolution) qui focalise les rayons perpendiculaires à la directrice de la parabole vers le foyer de la parabole. Montrons qu’effectivement cette contrainte impose une parabole, en effectuant une coupe par un plan passant par le foyer.
Rappel : une parabole est définie géométriquement par une droite D appelée directrice et un point O appelé foyer, c’est le lieu des points équidistants à D et O.
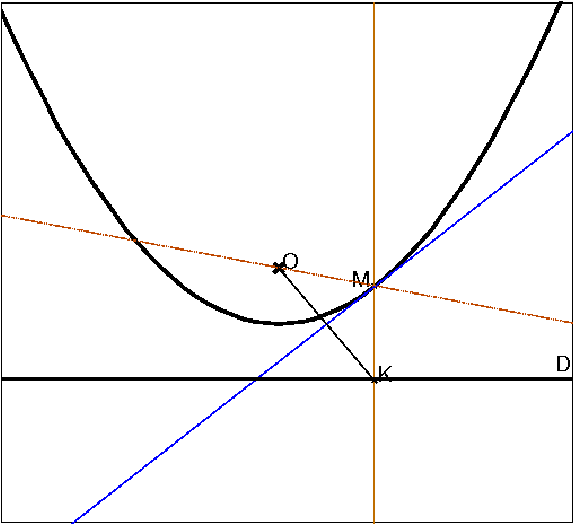
Figure 16: Parabole
Si on calcule l’équation de ce lieu, en prenant O comme origine, M(x,y) et l’équation de D sous la forme y=−m, on a
| x2+y2=OM2=d(M,D)2=(y+m)2=y2+2ym+m2 |
donc
| y= |
|
c’est bien l’équation usuelle d’une parabole. La normale à la parabole est obtenue en prenant le gradient de l’équation qui la définit
| OM−d(D,M)=0 |
c’est donc
| − |
| |||||||||||||||
qui est le vecteur directeur de la bissectrice de la verticale et de OM (plus précisément la bissectrice intérieure du vecteur OM et de −j ou de MO et de j). La tangente est donc la bissectrice extérieure de cet angle, ou encore la bissectrice intérieure de (MO,MK). On en déduit qu’un rayon vertical venant du haut se réfléchit sur la parabole symétriquement à la normale donc en passant par le foyer O.
Considérons maintenant une courbe ayant cette propriété: les rayons provenant du haut verticalement se réfléchissent dessus en passant par O. Soit M(x,y) un point de cette courbe. Prolongeons le rayon vertical passant par M vers le bas de la longueur OM, on obtient un point K d’ordonnée
| yk= y − | √ |
|
Montrons que lorsque x varie, yk a une dérivée nulle. On a :
| yk′= y′ − |
|
D’autre part, la tangente en M à la courbe est orthogonale à OK puisque c’est la bissectrice de l’angle (MO,MK) (hypothèse que le rayon réflechi passe par O) et que MO=MK (par construction de K), et le vecteur directeur de la tangente est (1,y′), on a donc
| (1,y′).(x,yk)=0 ⇒ x+y′y−y′ | √ |
| =0 |
donc yk′ est bien nul et K est donc sur une droite horizontale fixe D, d’où l’on déduit que M est sur la parabole de foyer O et directrice D, la courbe est donc forcément une parabole.
Rendement d’un tel système : on peut le définir comme le rapport de l’énergie focalisée sur la surface de miroir. Pour un miroir cylindrique avec une coupe parabolique, la surface est proportionnelle à la longueur de la courbe en coupe. On peut faire le calcul sur la parabole y=x2/2 pour déterminer par exemple quel portion de parabole on peut raisonnablement utiliser. Le cout de l’énergie est proportionnel à
| ∫ |
| √ |
| dx = |
| ⎛ ⎜ ⎜ ⎝ | √ |
| − |
| ln( | √ |
| −l) | ⎞ ⎟ ⎟ ⎠ |
Il ne faut pas prendre l trop grand (sinon le cout augmente trop vite), mais pas trop petit non plus (sinon on ne concentrera pas assez d’énergie pour avoir par exemple un bon rendement de Carnot). On peut aussi jouer sur le paramètre de la parabole (pour l’aplatir près de son point le plus bas, ce qui permet d’augmenter l à rendement constant), mais il faut alors augmenter l’altitude du foyer.
Ce système est bien adapté s’il reste petit, par exemple pour un four solaire pour faire la cuisson d’un repas, mais n’est pas adapté à de grandes installations, la taille du miroir parabolique à réaliser étant trop grande et trop difficile à manoeuvrer (toute l’installation doit bouger pour que la directrice de la parabole reste perpendiculaire aux rayons solaires). Pour une centrale solaire à concentration, le foyer doit être à une position fixe, et les miroirs doivent pouvoir être inclinés pour faire suivre les rayons du Soleil vers le foyer au cours de la journée. La direction miroir-foyer est donc fixe, et la direction miroir-Soleil imposée par la position du Soleil, le plan du miroir est déterminé par le point du miroir, la bissectrice extérieure aux 2 directions (dans le plan les contenant) et la perpendiculaire à ce plan. Ceci impose bien d’avoir des miroirs amovibles. L’énergie captée par ce système est proportionnel au cosinus de l’angle entre la normale au miroir et la direction miroir-Soleil. Comme la normale au miroir est la bissectrice intérieure de l’angle miroir-Soleil, miroir-foyer, l’énergie captée (par miroir) est proportionnelle au cosinus de la moitié de l’angle miroir-Soleil, miroir-foyer. On est donc ramené à un calcul analogue à celui du rendement de panneaux solaires thermiques, la normale au panneau étant remplacée par la direction miroir-foyer, mais on divise ensuite l’angle par 2.
Il y a actuellement deux grands freins au développement des énergies renouvelables : l’intermittence (conjointement avec la possibilité de stocker l’énergie) et la facon dont le coût est calculé. Le premier frein nécessite des avancées technologiques pour pouvoir monter en puissance, le deuxième ne me semble pas intrinsèque mais uniquement fondé sur la facon de financer un projet énergie renouvelables. En effet, un projet d’installation de panneaux solaires ou d’éoliennes nécessite un investissement important au départ (qui peut représenter jusqu’à plus de 90% du coût total par exemple pour des panneaux solaires thermiques) contrairement à un projet de centrale thermique au charbon ou au gaz. Comment doit-on répartir ce cout de manière juste sur la durée de fonctionnement de l’installation ? Les économistes utilisent un taux d’actualisation, ils comparent avec ce qu’une somme d’argent équivalente aurait pu rapporter en euros constants. Plus précisément le cout annuel estimé correspond à la moyenne des couts de fonctionnement plus le cout annuel qu’il faudrait payer pour rembourser en euros constants l’investissement initial. Le choix du taux d’actualisation est alors un paramètre très important qui peut faire varier du simple au double (voire plus) le coût estimé des énergies renouvelables. Les taux actuels de 5% à 10%, calculés sur la base d’une croissance soutenue de l’économie mondiale rendue possible par la hausse de la consommation mondiale d’énergie fossiles et l’amélioration de l’efficacité énergétique, paraissent peu compatibles avec une période de “plateau fossiles” voire de déplétion.
Les variations de concentration de gaz à effet de serre au cours du passé agissent sur le bilan énergétique de la Terre de manière logarithmique de l’ordre de quelques W/m2 (Watt par mètre carré), une valeur qui est du même ordre de grandeur que celles dues aux variations orbitales de la Terre ou que celles dues aux variations des volumes de glace (modification de l’albédo terrestre). La corrélation entre gaz à effet de serre et température calculée sur les 400 000 dernières années en Antarctique donne une sensibilité de 9 degrés pour 100 ppm de CO2 au niveau de l’Antarctique. En divisant ce chiffre par 2 pour tenir compte de la plus grande variabilité de la température en Antarctique puis par 3 pour tenir compte des 3 causes principales de variation de même importance (gaz à effet de serre, variations orbitales, volume des glaces), on obtient une sensibilité empirique de 1.5 degré pour 100ppm de CO2. Ce qui veut dire que si nous conservions la concentration actuelle en CO2 (100 ppm de plus qu’avant le début de l’ère industrielle en 2005), ce modèle prévoit une hausse de 1.5 degrés de la température, ce qui est parfaitement plausible avec l’élévation de 0.6 degrés du 20ème siècle (l’océan jouant le role de régulateur thermique de par son inertie sur des échelles de temps entre le siècle et le millénaire, par exemple le forçage radiatif actuel est estimé à plus de 2W/m2, or pour réchauffer l’océan de 1K avec une telle puissance il faut attendre plus de 200 ans, pour faire ce calcul, on considère qu’il y a une épaisseur moyenne de 3000 mètres d’eau, donc chaque heure, 2Wh servent à réchauffer 3000 mètre cubes d’eau, or il faut un peu plus d’un kWh pour réchauffer un mètre cube d’eau d’un degré, il faut donc environ 1,5 millions d’heures pour réchauffer l’océan à cette puissance).
Bien évidemment, une corrélation seule ne suffit pas à justifier l’existence d’une relation de cause à effet entre gaz à effet de serre et température, ce sont les lois de la physique qui justifient cette relation, la corrélation nous donne toutefois des informations quantitatives sur l’effet que l’on peut rapprocher des calculs issus de la physique. Ceux-ci donne un forçage radiatif de 4W par doublement du CO2 soit 0.3% de l’énergie reçue au sommet de l’atmosphère perpendiculairement au Soleil, ou encore 1.2% de l’énergie reçue au sommet de l’atmosphère en moyenne (pour tenir compte de la surface de la Terre 4π R2 qui est 4 fois plus grande que sa section perpendiculaire au Soleil π R2). En tenant compte de la partie du rayonnement arrivant effectivement dans les basses couches de l’atmosphère, c’est un forçage de 2 à 3%. Si la Terre était un corps noir à une température de 288K, ce forçage se traduirait par une hausse de plus de 0.5% de la température pour compenser (car la puissance émise par un corps noir est proportionnelle à T4, il faut donc diviser par 4 le forçage), donc de 2K environ. Ce chiffre est raisonnablement en accord avec les modèles du climat qui prévoient une hausse de 3 à 4K pour un doublement du CO2, en tenant compte des diverses rétroactions (modification de l’albédo par exemple).
Si nous voulons éviter une variation trop brusque de la température et plus encore des précipitations, il faut donc agir dès maintenant, ce qui ne sera pas facile car 1ppm de CO2 correspond à 2Gt de C soit à peine plus de 300kg de C par Terrien (ou un peu plus de 400 litres de pétrole) : rappelons qu’un Français consomme (en gros pour moitié directement par les transports et le chauffage, et l’autre moitié indirectement par la consommation de biens) en moyenne 1.5 tep de pétrole, 0.67 tep de gaz et 0.2 tep de charbon par an, il émet donc 2 tonnes de C par an (ce qui généralisé à l’échelle de la planète correspondrait à une émission de 6 ppmv de CO2 par an).
http://www.imcce.fr/fr/presentation/equipes/ASD/insola/earth/earth.html
http://www.ens-lyon.fr/Planet-Terre/Infosciences/Histoire/Paleoclimats/
http://www.ipcc.ch/
www.realclimate.org
http://www.ncdc.noaa.gov/paleo/recons.html,
ftp://ftp.ncdc.noaa.gov/pub/data/paleo/icecore/antarctica/vostok/,
le fichier ch4nat.txt contient les données pour le méthane, co2nat.txt
pour le CO2, deutnat.txt pour la température.
(remonter d’un cran dans l’arborescence du site pour d’autres lieux).
ftp://ftp.ncdc.noaa.gov/pub/data/paleo/icecore/antarctica/epica_domec/
http://data.giss.nasa.gov/http://hydrolab.arsusda.gov/nicks/nicks.htm
http://cdiac.esd.ornl.gov/ftp/trends/co2/maunaloa.co2
http://www.industrie.gouv.fr/energie/sommaire.htm
http://www.theoildrum.com/
http://aspofrance.org/,
http://www.ifp.fr
http://www.manicore.com/
(D’après Frédéric Faure). La rotation de la Terre a pour conséquence qu’elle n’est pas sphérique. En effet, la force centrifuge vaut mω2 r, où r est le vecteur issu de la projection sur l’axe de rotation et ω=2π/1 jour est la vitesse angulaire. Cette force dérive du potentiel −m ω2 r2/2 qu’il faut ajouter au potentiel dû à la gravité, en première approximation mgh où h+R est la distance au centre de la Terre, (R étant la distance moyenne de la surface de la Terre à son centre). Si l’on ne tient pas compte de la force centrifuge, h=0 pour avoir un potentiel identiquement nul sur toute la surface, on a une sphère. Si l’on en tient compte, ce ne sera pas le cas sauf aux poles (où r=0). Ainsi à l’équateur, pour avoir un potentiel nul, il faut prendre h= ω2 R2/(2g), soit h=11km environ, il y a donc un bourrelet un peu plus épais au niveau de l’équateur. En réalité, on observe un aplatissement de l’ordre du double, l’approximation du potentiel de gravitation n’est en effet pas très bonne, parce qu’elle suppose une Terre sphérique, ce qui n’est pas le cas comme on vient de le voir.
L’existence d’un bourrelet équatorial et l’inclinaison de l’axe
de rotation de la Terre par rapport au plan de l’orbite terrestre entraine
l’existence d’un couple exercé par le Soleil et la Lune sur la Terre.
Ce couple s’exerce dans des plans contenant l’axe de rotation de la Terre
(qui est axe de symétrie)
et a donc un moment perpendiculaire à l’axe de rotation. Les
équations du mouvement (dérivée du moment cinétique
donc de la vitesse angulaire = moment du couple) entrainent alors que la
dérivée du vecteur rotation est perpendiculaire
à l’axe de rotation
(et cette dérivée est petite), le vecteur rotation conserve
donc sa norme au cours du temps mais sa direction bouge lentement
perpendiculairement à lui-même. Cela entraine en un an une petite
rotation du vecteur rotation de la Terre sur un cone autour
de la perpendiculaire au plan de l’orbite. On peut faire
le calcul en modélisant la Terre par un ellipsoide de révolution
(cf. par exemple
www-fourier.ujf-grenoble.fr/~faure/enseignement/
puis meca_analytique_L3/index.html#Travaux_dirig%E9s),
et on montre que l’action du Soleil et de la Lune s’additionne
pour faire faire un tour complet à l’axe de rotation de la Terre
autour de la perpendiculaire au plan de l’orbite en un peu
moins de 26 000 ans. C’est la précession astronomique.
Le problème se complique si on considére les autres planètes du système solaire, en particulier Jupiter. En effet l’orbite elliptique de la Terre se déforme au cours des millénaires, en particulier la position de l’axe des foyers, donc la direction de l’axe aphélie-périhélie, or c’est l’angle entre cet axe et la projection de l’axe de rotation de la Terre qui importe pour les variations des saisons. C’est pour cette raison que la périodicite de la précession “climatique” est un peu plus courte que la précession astronomique.
Ce document a été traduit de LATEX par HEVEA